题目内容
(本小题满分12分) 设不等式组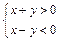 表示的平面区域为
表示的平面区域为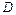 ,区域
,区域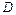 内的动点
内的动点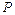 到直线
到直线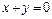 和直线
和直线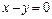 的距离之积为2, 记点
的距离之积为2, 记点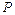 的轨迹为曲线
的轨迹为曲线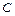 . 是否存在过点
. 是否存在过点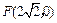 的直线l, 使之与曲线
的直线l, 使之与曲线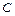 交于相异两点
交于相异两点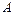 、
、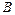 ,且以线段
,且以线段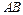 为直径的圆与y轴相切?若存在,求出直线l的斜率;若不存在, 说明理由.
为直径的圆与y轴相切?若存在,求出直线l的斜率;若不存在, 说明理由.
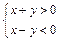 表示的平面区域为
表示的平面区域为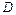 ,区域
,区域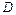 内的动点
内的动点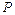 到直线
到直线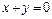 和直线
和直线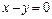 的距离之积为2, 记点
的距离之积为2, 记点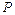 的轨迹为曲线
的轨迹为曲线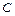 . 是否存在过点
. 是否存在过点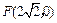 的直线l, 使之与曲线
的直线l, 使之与曲线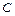 交于相异两点
交于相异两点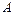 、
、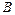 ,且以线段
,且以线段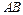 为直径的圆与y轴相切?若存在,求出直线l的斜率;若不存在, 说明理由.
为直径的圆与y轴相切?若存在,求出直线l的斜率;若不存在, 说明理由. k=-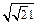
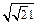
由题意可知,平面区域 如图阴影所示.设动点为
如图阴影所示.设动点为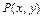 ,则
,则
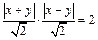 ,即
,即

 .
.
由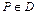 知
知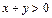 ,x-y<0,即x2-y2<0.
,x-y<0,即x2-y2<0.
所以y2-x2=4(y>0),即曲线 的方程为
的方程为
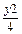 -
-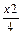 =1(y>0)
=1(y>0)
设 ,
, ,则以线段
,则以线段 为直径的圆的圆心为
为直径的圆的圆心为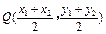 .
.
因为以线段 为直径的圆
为直径的圆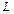 与
与 轴相切,所以半径
轴相切,所以半径  ,即
,即

因为直线AB过点F(2 ,0),当AB ^x轴时,不合题意.所以设直线AB的方程为y=k(x-2
,0),当AB ^x轴时,不合题意.所以设直线AB的方程为y=k(x-2 ).代入双曲线方程
).代入双曲线方程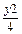 -
-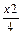 =1(y>0)得:
=1(y>0)得:
k2(x-2 )2-x2=4,即
)2-x2=4,即
(k2-1)x2-4 k2x+(8k2-4)=0.
k2x+(8k2-4)=0.
因为直线与双曲线交于A,B两点,所以k≠±1.于是
x1+x2= ,x1x2=
,x1x2= .
.
故 |AB|= =
=
=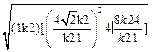 =|x1+x2|=|
=|x1+x2|=| |,
|,
化简得:k4+2k2-1=0
解得: k2= -1 (k2=-
-1 (k2=- -1不合题意,舍去).
-1不合题意,舍去).
由△=(4 k2)2-4(k2-1)(8k2-4)=3k2-1>0,又由于y>0,所以-1<k<-
k2)2-4(k2-1)(8k2-4)=3k2-1>0,又由于y>0,所以-1<k<-  .
.
所以, k=-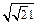
 如图阴影所示.设动点为
如图阴影所示.设动点为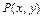 ,则
,则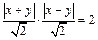 ,即
,即
 .
.由
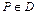 知
知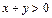 ,x-y<0,即x2-y2<0.
,x-y<0,即x2-y2<0.所以y2-x2=4(y>0),即曲线
 的方程为
的方程为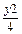 -
-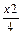 =1(y>0)
=1(y>0) 设
 ,
, ,则以线段
,则以线段 为直径的圆的圆心为
为直径的圆的圆心为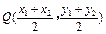 .
. 因为以线段
 为直径的圆
为直径的圆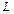 与
与 轴相切,所以半径
轴相切,所以半径  ,即
,即
因为直线AB过点F(2
 ,0),当AB ^x轴时,不合题意.所以设直线AB的方程为y=k(x-2
,0),当AB ^x轴时,不合题意.所以设直线AB的方程为y=k(x-2 ).代入双曲线方程
).代入双曲线方程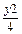 -
-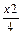 =1(y>0)得:
=1(y>0)得:k2(x-2
 )2-x2=4,即
)2-x2=4,即(k2-1)x2-4
 k2x+(8k2-4)=0.
k2x+(8k2-4)=0.因为直线与双曲线交于A,B两点,所以k≠±1.于是
x1+x2=
 ,x1x2=
,x1x2= .
.故 |AB|=
 =
=
=
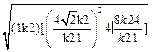 =|x1+x2|=|
=|x1+x2|=| |,
|,化简得:k4+2k2-1=0
解得: k2=
 -1 (k2=-
-1 (k2=- -1不合题意,舍去).
-1不合题意,舍去).由△=(4
 k2)2-4(k2-1)(8k2-4)=3k2-1>0,又由于y>0,所以-1<k<-
k2)2-4(k2-1)(8k2-4)=3k2-1>0,又由于y>0,所以-1<k<-  .
.所以, k=-
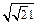

练习册系列答案
相关题目
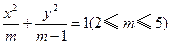 ,过其左焦点且斜率为
,过其左焦点且斜率为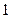 的直线与椭圆及其准线的交点从左到右的顺序为
的直线与椭圆及其准线的交点从左到右的顺序为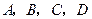 (如图),设
(如图),设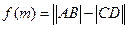 .
.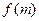 的解析式;
的解析式;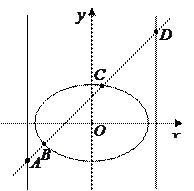
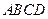 中,
中, ,
,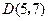 ,中心
,中心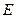 在第一象限内,且与
在第一象限内,且与 轴的距离为一个单位,动点
轴的距离为一个单位,动点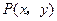 沿矩形一边
沿矩形一边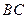 运动,求
运动,求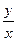 的取值范围.
的取值范围.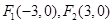 ,一条渐近线方程为
,一条渐近线方程为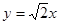 ,则该双曲线的方程为________________
,则该双曲线的方程为________________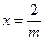
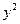 (
(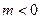 )与椭圆
)与椭圆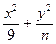 =1有一个相同的焦点,则动点
=1有一个相同的焦点,则动点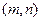 的轨迹是( )
的轨迹是( ) 双曲线的一部分
双曲线的一部分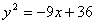 的顶点和准线.
的顶点和准线.  ,求点P到x轴的距离;
,求点P到x轴的距离; .椭圆
.椭圆  .直线
.直线
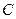 .线段
.线段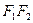
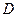 .线段
.线段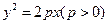 的对称轴上一点
的对称轴上一点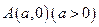 的直线与抛物线相交于M、N两点,自M、N向直线
的直线与抛物线相交于M、N两点,自M、N向直线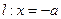 作垂线,垂足分别为
作垂线,垂足分别为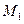 、
、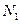 。
。 

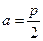 时,求证:
时,求证: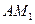 ⊥
⊥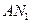 ;
;
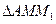 、
、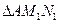 、
、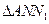 的面积分别为
的面积分别为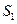 、
、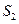 、
、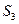 ,是否存在
,是否存在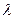 ,使得对任意的
,使得对任意的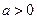 ,都有
,都有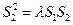 成立。若存在,求出
成立。若存在,求出