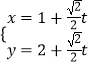题目内容
【题目】四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠DAB= ![]() ,AC∩BD=O,且PO⊥平面ABCD,PO=
,AC∩BD=O,且PO⊥平面ABCD,PO= ![]() ,点F,G分别是线段PB,PD上的中点,E在PA上,且PA=3PE.
,点F,G分别是线段PB,PD上的中点,E在PA上,且PA=3PE. 
(Ⅰ)求证:BD∥平面EFG;
(Ⅱ)求直线AB与平面EFG的成角的正弦值;
(Ⅲ)请画出平面EFG与四棱锥的表面的交线,并写出作图的步骤.
【答案】证明:(Ⅰ)在△PBD中, ∵点F,G分别是线段PB,PD上的中点,
∴FG∥BD,
∵BD平面EFG,FG平面EFG,
∴BD∥平面EFG.
解:(Ⅱ)∵底面ABCD是边长为2的菱形,
∴OA⊥OB,
∵PO⊥平面ABCD,∴PO⊥OA,PO⊥OB,
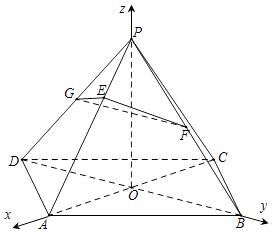
如图,以O为原点,OA、OB、OP分别为x,y,z轴,
建立空间直角坐标系,
则 ![]() ,
, 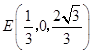 ,
, 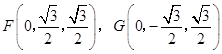 ,
,
∴ ![]() ,
, 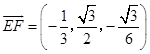 ,
, ![]() ,
,
设平面EFG的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 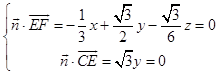 ,令
,令 ![]() ,得
,得 ![]() =(﹣
=(﹣ ![]() ),
),
∵cos< ![]() ,
, ![]() >=
>= 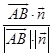 =
= ![]() ,
,
∴直线AB与平面EFG的成角的正弦值为 ![]() .
.
(Ⅲ)法1:延长EF,EG分别交AB,AD延长线于M,N,连接MN,发现刚好过点C,
连接CG,CF,
则四边形EFCG为平面EFG与四棱锥的表面的交线.
法2:记平面EFG与直线PC的交点为H,设 ![]() ,
,
则 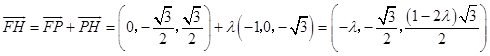
由 ![]() =(﹣
=(﹣ ![]() )(﹣
)(﹣ ![]() )=0,解得λ=1.
)=0,解得λ=1.
所以H即为点C.
所以连接CG,CF,则四边形EFCG为平面EFG与四棱锥的表面的交线.
【解析】(Ⅰ)推导出FG∥BD,由此能证明BD∥平面EFG. (Ⅱ)推导出OA⊥OB,PO⊥OA,PO⊥OB,以O为原点,OA、OB、OP分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出直线AB与平面EFG的成角的正弦值.(Ⅲ)法1:延长EF,EG分别交AB,AD延长线于M,N,连接MN,发现刚好过点C,连接CG,CF,则四边形EFCG为平面EFG与四棱锥的表面的交线.
法2:记平面EFG与直线PC的交点为H,设 ![]() ,利用向量法求出λ=1.从而H即为点C.连接CG,CF,则四边形EFCG为平面EFG与四棱锥的表面的交线.
,利用向量法求出λ=1.从而H即为点C.连接CG,CF,则四边形EFCG为平面EFG与四棱锥的表面的交线.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.