Question

【题目】已知函数f（x）=|sinx|+cosx，现有如下几个命题： ①该函数为偶函数；
②该函数最小正周期为 ；
③该函数值域为 ；
④若定义区间（a，b）的长度为b﹣a，则该函数单调递增区间长度的最大值为 ．
其中正确命题为 ．

Answer 1

【答案】①③④
【解析】解：当sinx≥0，即2kπ≤x≤2kπ+π，k∈Z，此时f（x）=sinx+cosx= sin（x+ ）， 当sinx＜0，即2kπ﹣π≤x≤2kπ，k∈Z，此时f（x）=﹣sinx+cosx= cos（x+ ），①f（﹣x）=|sin（﹣x）|+cosx=|sinx|+cosx=f（x），则函数f（x）是偶函数，故①正确，②f（x+ ）=|sin（x+ ）|+cos（x+ ）=|cosx|﹣sinx≠f（x），则函数最小正周期为 错误，故②错误，
当2kπ≤x≤2kπ+π时，2kπ+ ≤x+ ≤2kπ+ ，此时 sin（x+ ）∈[﹣1， ]，
当2kπ﹣π≤x≤2kπ时，2kπ ≤x+ ≤2kπ+ ，此时 cos（x+ ）∈[﹣1， ]，
综上f（x））∈[﹣1， ]，即函数的值域为[﹣1， ]，故③正确，④作出函数f（x）的图象如图：

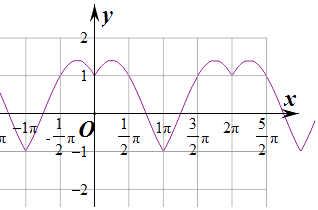
函数单调递增的最大区间在函数f（x）= cos（x+ ），
由2kπ﹣π≤x+ ≤2kπ，k∈Z得2kπ﹣ ≤x≤2kπ﹣ ，k∈Z
∵2kπ﹣π≤x≤2kπ，∴此时2kπ﹣π≤x≤2kπ﹣ ，即此时函数的单调递增区间为[2kπ﹣π，2kπ﹣ ]，
当k=0时，单调递增区间为[﹣π，﹣ ]，此时区间长度为﹣ ﹣（﹣π）= ，
故④正确，
所以答案是：①③④．
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点，需要掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系才能正确解答此题．