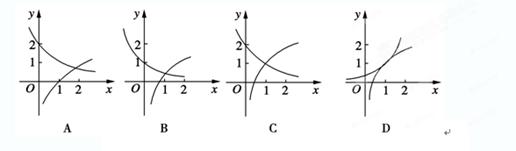
题目内容
已知函数 ,则方程
,则方程 恰有两个不同实数根时,实数
恰有两个不同实数根时,实数 的取值范围是( )(注:
的取值范围是( )(注: 为自然对数的底数)
为自然对数的底数)
A. | B. | C. | D. |
C
解析试题分析:∵方程 恰有两个不同实数根,∴
恰有两个不同实数根,∴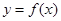 与
与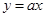 有2个交点,∵
有2个交点,∵ 表示直线
表示直线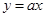 的斜率,∴
的斜率,∴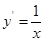 ,设切点为
,设切点为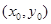 ,
,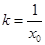 ,所以切线方程为
,所以切线方程为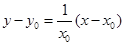 ,而切线过原点,所以
,而切线过原点,所以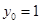 ,
,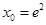 ,
,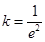 ,所以直线
,所以直线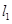 的斜率为
的斜率为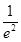 ,直线
,直线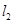 与
与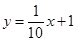 平行,所以直线
平行,所以直线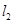 的斜率为
的斜率为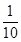 ,所以当直线在
,所以当直线在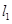 和
和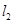 之间时,符合题意,所以实数
之间时,符合题意,所以实数 的取值范围是
的取值范围是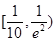 ,还有一部分是在
,还有一部分是在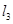 的位置向下旋转一直到转平为止都符合题意,这时实数
的位置向下旋转一直到转平为止都符合题意,这时实数 的取值范围是
的取值范围是 ,所以综上所述,实数
,所以综上所述,实数 的取值范围是
的取值范围是 .
.
考点:1.分段函数图象;2.利用导数求曲线的切线方程;3.图象的交点问题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
已知函数
 满足
满足 ,且
,且 时,
时, ,则当
,则当 时,
时, 与
与 的图象的交点个数为( )
的图象的交点个数为( )
| A.13 | B.12 | C.11 | D.10 |
设函数 对任意的
对任意的 满足
满足 ,当
,当 时,有
时,有 .若函数
.若函数 在区间
在区间 上有零点,则k的值为
上有零点,则k的值为
| A.-3或7 | B.-4或7 | C.-4或6 | D.-3或6 |
己知函数f(x)= 在[-1,1]上的最大值为M(a) ,若函数g(x)=M(x)-
在[-1,1]上的最大值为M(a) ,若函数g(x)=M(x)- 有4个零点,则实数t的取值范围为( )
有4个零点,则实数t的取值范围为( )
A.(1, ) ) | B.( 1,-1) 1,-1) |
C.( 1,-1) 1,-1) (1, (1,  ) ) | D.( 1,-1) 1,-1) (1,2) (1,2) |
函数 的定义域为( )
的定义域为( )
A. | B. |
C. | D. |
已知函数

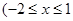 且
且 ),则
),则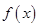 的值域是 ( )
的值域是 ( )
A. | B.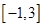 | C. | D. |
定义在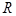 上的函数
上的函数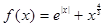 ,且
,且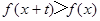 在
在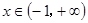 上恒成立,则关于
上恒成立,则关于 的方程
的方程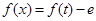 的根的个数叙述正确的是( )
的根的个数叙述正确的是( )
| A.有两个 | B.有一个 | C.没有 | D.上述情况都有可能 |
 ,若方程
,若方程 有且只有两个不相等的实数根,则实数a的取值范围为 ( )
有且只有两个不相等的实数根,则实数a的取值范围为 ( ) B、
B、 C、
C、 D、
D、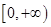 。
。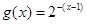 在同一直角坐标系下的图像大致是 ( )
在同一直角坐标系下的图像大致是 ( )