Question

已知椭圆的左、右焦点分别为F₁、F₂，短轴端点分别为A、B，且四边形F₁AF₂B是边长为2的正方形

 （I）求椭圆的方程；

 （II）若C、D分别是椭圆长轴的左、右端点，动点M满足，连结CM交椭圆于P，证明为定值（O为坐标原点）；_K^S*5U.C#O%

 （III）在（II）的条件下，试问在x轴上是否存在异于点C的定点Q，使以线段MP为直径的圆恒过直线DP、MQ的交点，若存在，求出Q的坐标，若不存在，说明理由

 

 

 

 

 

 

 

Answer 1

【答案】

【解析】

（1）如图，由题知，……3分

（2）C(-2,0),D(2,0),

则可设…5分

                         

 

 

 

 

 

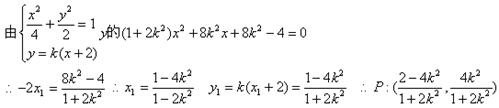
 …………9分

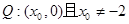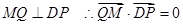   （3）设，由题知成立

使得以MP为直径的圆恒过DP、MQ的交点  ………………13分