题目内容
如图,四棱锥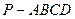 中,
中,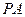 ⊥平面
⊥平面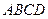 ,
,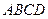 是矩形,
是矩形,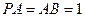 ,
,
直线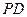 与底面
与底面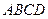 所成的角等于30°,
所成的角等于30°,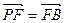 ,
, 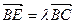
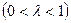 .
.
(1)若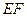 ∥平面
∥平面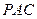 ,求
,求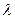 的值;
的值;
(2)当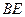 等于何值时,二面角
等于何值时,二面角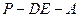 的大小为45°?
的大小为45°?

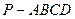 中,
中,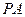 ⊥平面
⊥平面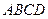 ,
,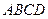 是矩形,
是矩形,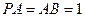 ,
,直线
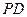 与底面
与底面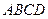 所成的角等于30°,
所成的角等于30°,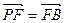 ,
, 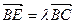
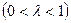 .
.(1)若
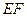 ∥平面
∥平面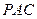 ,求
,求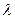 的值;
的值;(2)当
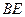 等于何值时,二面角
等于何值时,二面角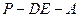 的大小为45°?
的大小为45°?
解:(1)∵平面PBC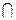 平面PAC=AC,EF
平面PAC=AC,EF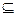 平面PBC,若EF∥平面PAC,
平面PBC,若EF∥平面PAC,
则EF∥PC,又F是PB的中点,∴E为BC的中点,∴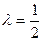 ………4分
………4分
(2)以A为坐标原点,分别以AD、AB、AP所在直线为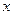 轴、
轴、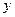 轴、
轴、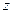 轴
轴
建立空间直角坐标系,则P(0,0,1),B(0,1,0),F(0,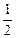 ,
,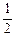 ),
),
D(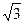 ,0,0), 设
,0,0), 设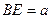 ,则E(
,则E(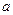 ,1,0)
,1,0)
求得平面PDE的法向量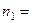 (
(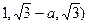 ,平面ADE的法向量
,平面ADE的法向量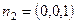 ,…8分
,…8分
∴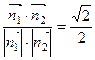 ,
,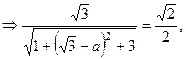
解得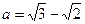 或
或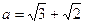 (舍去),
(舍去),
所以当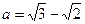 时,二面角
时,二面角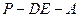 的大小45°。
的大小45°。
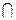 平面PAC=AC,EF
平面PAC=AC,EF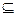 平面PBC,若EF∥平面PAC,
平面PBC,若EF∥平面PAC,则EF∥PC,又F是PB的中点,∴E为BC的中点,∴
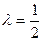 ………4分
………4分(2)以A为坐标原点,分别以AD、AB、AP所在直线为
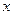 轴、
轴、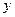 轴、
轴、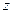 轴
轴建立空间直角坐标系,则P(0,0,1),B(0,1,0),F(0,
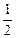 ,
,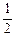 ),
),D(
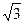 ,0,0), 设
,0,0), 设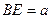 ,则E(
,则E(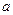 ,1,0)
,1,0)求得平面PDE的法向量
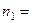 (
(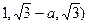 ,平面ADE的法向量
,平面ADE的法向量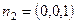 ,…8分
,…8分∴
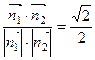 ,
,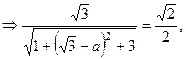
解得
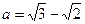 或
或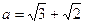 (舍去),
(舍去),所以当
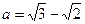 时,二面角
时,二面角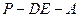 的大小45°。
的大小45°。略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
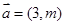 ,
,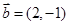 ,,
,, 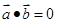 ,则实数
,则实数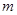 的值为( )
的值为( )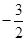
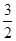
 ,在四棱锥S—ABCD中,底面ABCD为矩形,SA⊥平面ABCD,SA=AD,M为AB中点,N为SC中点.
,在四棱锥S—ABCD中,底面ABCD为矩形,SA⊥平面ABCD,SA=AD,M为AB中点,N为SC中点. D;
D;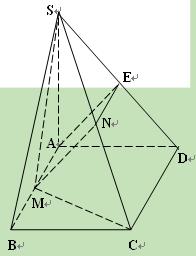
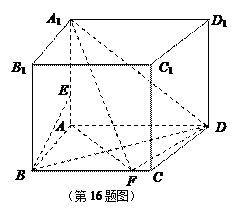
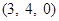 ,
, 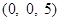
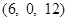 ,
,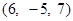
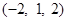 ,
, 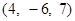
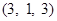 ,
, 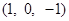
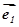 ,
,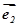 是两个相互垂直的单位向量,一直角三角形两条边所对应的向量分别为
是两个相互垂直的单位向量,一直角三角形两条边所对应的向量分别为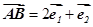 ,
,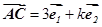 ,
,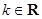 ,则
,则 的值可能是( )
的值可能是( )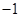 或
或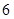
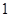 或
或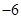
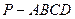 的底面为直角梯形,
的底面为直角梯形,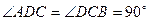 ,
,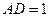 ,
,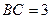 ,
,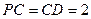 ,
,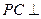 平面
平面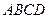
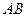 上是否存在一点
上是否存在一点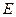 ,使平面
,使平面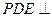 平面
平面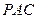 ,并说明理由;
,并说明理由;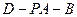 的余弦值.
的余弦值.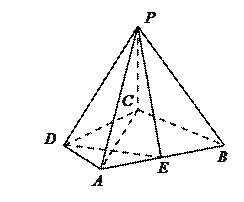
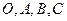 满足
满足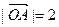 ,
,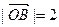 ,
,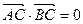 ,则
,则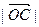 的最大值为 .
的最大值为 .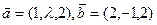 ,且
,且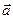 与
与 的夹角余弦为
的夹角余弦为 ,则
,则 等于_________________.
等于_________________.