题目内容
设定义在R上的函数f(x)=ax3+bx2+cx,当 时,f(x)取得极大值
时,f(x)取得极大值 ,并且函数y=f'(x)的图象关于y轴对称.
,并且函数y=f'(x)的图象关于y轴对称.(1)求f(x)的表达式;
(2)若曲线C对应的解析式为
 ,求曲线C过点P(2,4)的切线方程;
,求曲线C过点P(2,4)的切线方程;(3)(实)过点
 可作曲线y=f(x)的三条切线,求实数m的取值范围.
可作曲线y=f(x)的三条切线,求实数m的取值范围.
【答案】分析:(1)由f′(x)=3ax2+2bx+c为偶函数,得到b=0,再由当 时,f(x)取得极大值
时,f(x)取得极大值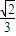 ,解得 a=
,解得 a= ,c=-1,由此能求出f(x).
,c=-1,由此能求出f(x).
(2) =
=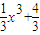 ,设切点为(x,y),则y=
,设切点为(x,y),则y= ,由此能求出切线方程.
,由此能求出切线方程.
(3)设切点坐标为(t, ),切线方程为:y-
),切线方程为:y- =(2t2-1)(x-t),把A(1,m)代入,得
=(2t2-1)(x-t),把A(1,m)代入,得 =0,由过点
=0,由过点 可作曲线y=f(x)的三条切线,知
可作曲线y=f(x)的三条切线,知 =0有三个解,由此能求出实数m的取值范围.
=0有三个解,由此能求出实数m的取值范围.
解答:解:(1)∵f′(x)=3ax2+2bx+c为偶函数,∴f(x)=f(-x),
∴3ax2-2bx+c=3ax2+2bx+c,
∴2bx=0得到b=0,
∴f(x)=ax3+cx,
∵当 时,f(x)取得极大值
时,f(x)取得极大值 ,
,
∴ ,
,
∴解得 a= ,c=-1,
,c=-1,
∴f(x)= -x.
-x.
(2)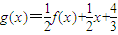 =
= ,
,
设切点为(x,y),则y= ,k=g′(x)|
,k=g′(x)| =x
=x ,
,
切线方程为:y-( +
+ )=
)= (x-x),
(x-x),
代入点P(2,4)化简得:x -3x
-3x +4=0,解得x=-1,或x=2,
+4=0,解得x=-1,或x=2,
所以切线方程为:x-y+2=0或4x-y-4=0.
(3)设切点坐标为(t, ),
),
∵f(x)= -x,∴f′(x)=2x2-1,
-x,∴f′(x)=2x2-1,
则切线方程为:y- =(2t2-1)(x-t),
=(2t2-1)(x-t),
把A(1,m)代入,得m- =(2t2-1)(1-t),
=(2t2-1)(1-t),
整理,得 =0,
=0,
∵过点 可作曲线y=f(x)的三条切线,
可作曲线y=f(x)的三条切线,
∴ =0有三个解,
=0有三个解,
记g(t)= ,
,
则g′(t)=4t2-4t,
令g′(t)=4t2-4t=0,得t=0,或t=1,
列表讨论,
∴当t=0时,g(t)取极大值g(0)=m+1,
当t=1时,g(t)取极小值g(1)=m+ ,
,
要使g(t)有三个零点,只需m+1>0且m+ <0,解得-1<m<-
<0,解得-1<m<- .
.
∴实数m的取值范围是(-1,- ).
).
点评:本题考查函数表达式的求法,考查切线方程的求法,考查实数的取值范围的求法.解题时要认真审题,仔细解答,注意导数性质的灵活运用.
 时,f(x)取得极大值
时,f(x)取得极大值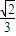 ,解得 a=
,解得 a= ,c=-1,由此能求出f(x).
,c=-1,由此能求出f(x).(2)
 =
=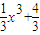 ,设切点为(x,y),则y=
,设切点为(x,y),则y= ,由此能求出切线方程.
,由此能求出切线方程.(3)设切点坐标为(t,
 ),切线方程为:y-
),切线方程为:y- =(2t2-1)(x-t),把A(1,m)代入,得
=(2t2-1)(x-t),把A(1,m)代入,得 =0,由过点
=0,由过点 可作曲线y=f(x)的三条切线,知
可作曲线y=f(x)的三条切线,知 =0有三个解,由此能求出实数m的取值范围.
=0有三个解,由此能求出实数m的取值范围.解答:解:(1)∵f′(x)=3ax2+2bx+c为偶函数,∴f(x)=f(-x),
∴3ax2-2bx+c=3ax2+2bx+c,
∴2bx=0得到b=0,
∴f(x)=ax3+cx,
∵当
 时,f(x)取得极大值
时,f(x)取得极大值 ,
,∴
 ,
,∴解得 a=
 ,c=-1,
,c=-1,∴f(x)=
 -x.
-x.(2)
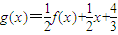 =
= ,
,设切点为(x,y),则y=
 ,k=g′(x)|
,k=g′(x)| =x
=x ,
,切线方程为:y-(
 +
+ )=
)= (x-x),
(x-x),代入点P(2,4)化简得:x
 -3x
-3x +4=0,解得x=-1,或x=2,
+4=0,解得x=-1,或x=2,所以切线方程为:x-y+2=0或4x-y-4=0.
(3)设切点坐标为(t,
 ),
),∵f(x)=
 -x,∴f′(x)=2x2-1,
-x,∴f′(x)=2x2-1,则切线方程为:y-
 =(2t2-1)(x-t),
=(2t2-1)(x-t),把A(1,m)代入,得m-
 =(2t2-1)(1-t),
=(2t2-1)(1-t),整理,得
 =0,
=0,∵过点
 可作曲线y=f(x)的三条切线,
可作曲线y=f(x)的三条切线,∴
 =0有三个解,
=0有三个解,记g(t)=
 ,
,则g′(t)=4t2-4t,
令g′(t)=4t2-4t=0,得t=0,或t=1,
列表讨论,
| t | (-∞,0) | 0 | (0,1) | 1 | (1,+∞) |
| g′(t) | + | 0 | - | 0 | + |
| g(t) | ↑ | 极大值 | ↓ | 极小值 | ↑ |
当t=1时,g(t)取极小值g(1)=m+
 ,
,要使g(t)有三个零点,只需m+1>0且m+
 <0,解得-1<m<-
<0,解得-1<m<- .
.∴实数m的取值范围是(-1,-
 ).
).点评:本题考查函数表达式的求法,考查切线方程的求法,考查实数的取值范围的求法.解题时要认真审题,仔细解答,注意导数性质的灵活运用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
设定义在R上的函数f(x)同时满足以下条件:①f(x+1)=-f(x)对任意的x都成立;②当x∈[0,1]时,f(x)=ex-e•cos
+m(其中e=2.71828…是自然对数的底数,m是常数).记f(x)在区间[2013,2016]上的零点个数为n,则( )
| πx |
| 2 |
A、m=-
| ||
| B、m=1-e,n=5 | ||
C、m=-
| ||
| D、m=e-1,n=4 |