Question

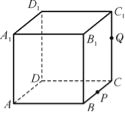
【题目】如图所示，四棱柱中，侧棱底面，，，，，为的中点.

（1）证明：；

（2）求二面角的正弦值；

（3）设点在线段上，且直线与平面所成角的正弦值为，求线段的长.

Answer 1

【答案】（1）证明见解析；（2）；（3）.

【解析】

试题分析：（1）根据线面垂直有，计算得，即，所以平面，所以；（2）过作于点，连接.由（1）知，，故平面，得.∴为二面角的平面角.在中计算得；（3）连接，过点作于点，可得平面，连接，则为直线与平面所成的角.设，在中利用余弦定理建立关于的方程，求得.

试题解析：

（1）∵侧棱底面，平面，∴.

经计算可得，，，

∴，∴在中，.

又∵，平面，，∴平面.又平面，

∴.

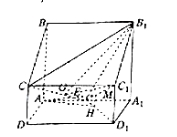
（2）如图所示，过作于点，连接.

由（1）知，，故平面，得.

∴为二面角的平面角.

在中，由，，可得.

在中，，∴，

即二面角的正弦值为.

（3）如图所示，连接，过点作于点，可得平面，

连接，则为直线与平面所成的角.

设，从而在中，有，.

在中，，，得.

在中，，，

由，

得，

整理得，解得（负值舍去）.

∴线段的长为.