题目内容
已知抛物线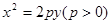 过点
过点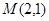 .
.
(I)求抛物线的方程;
(II)已知圆心在 轴上的圆
轴上的圆 过点
过点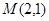 ,且圆
,且圆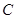 在点
在点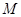 的切线恰是抛物线在点
的切线恰是抛物线在点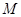 的切线,求圆
的切线,求圆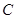 的方程;
的方程;
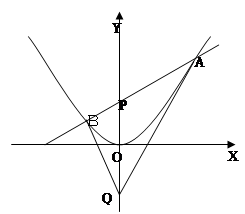
(Ⅲ)如图,点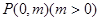 为
为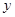 轴上一点,点
轴上一点,点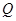 是点
是点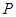 关于原点的对称点,过点
关于原点的对称点,过点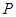 作一条直线与抛物线交于
作一条直线与抛物线交于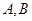 两点,若
两点,若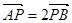 ,证明:
,证明: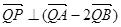 .
.
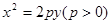 过点
过点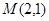 .
.(I)求抛物线的方程;
(II)已知圆心在
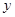 轴上的圆
轴上的圆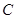 过点
过点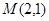 ,且圆
,且圆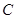 在点
在点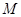 的切线恰是抛物线在点
的切线恰是抛物线在点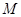 的切线,求圆
的切线,求圆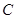 的方程;
的方程;(Ⅲ)如图,点
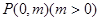 为
为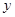 轴上一点,点
轴上一点,点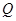 是点
是点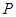 关于原点的对称点,过点
关于原点的对称点,过点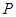 作一条直线与抛物线交于
作一条直线与抛物线交于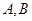 两点,若
两点,若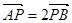 ,证明:
,证明: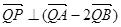 .
.
(I)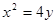 ;(II)
;(II)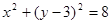 ;(Ⅲ)见解析。
;(Ⅲ)见解析。
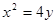 ;(II)
;(II)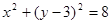 ;(Ⅲ)见解析。
;(Ⅲ)见解析。试题分析:(I)
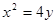
(II)由
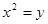 得
得 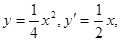 所以抛物线
所以抛物线 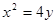 在点
在点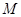 处切线的斜率为
处切线的斜率为
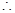 过点
过点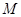 且与切线垂直的直线方程为:
且与切线垂直的直线方程为: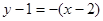 ,即
,即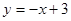 ,令
,令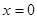 得
得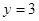
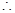 圆心
圆心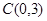 ,半径
,半径
圆
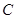 的方程为:
的方程为: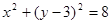
(Ⅲ)设直线AB的方程为
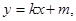 代入抛物线方程
代入抛物线方程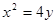 得
得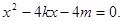
设A、B两点的坐标分别是
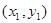 、
、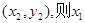 、x2是方程①的两根.
、x2是方程①的两根.所以
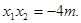 ①
① 由
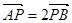 得
得 即
即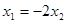 ②
②由①、②可得
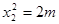
又点Q是点P关于原点的对称点,故点Q的坐标是(0,-m),从而
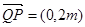 .
.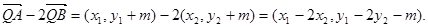
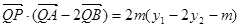
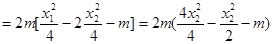
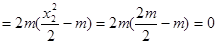
所以
点评::研究直线与抛物线的综合问题,通常的思路是:转化为研究方程组的解的问题,利用直线方程与抛物线方程所组成的方程组消去一个变量后,将交点问题(包括公共点个数、与交点坐标有关的问题)转化为一元二次方程根的问题,结合根与系数的关系及判别式解决问题。

练习册系列答案
相关题目
 的四个顶点
的四个顶点 构成的四边形为菱形,若菱形
构成的四边形为菱形,若菱形 的内切圆恰好过焦点,则椭圆的离心率是
的内切圆恰好过焦点,则椭圆的离心率是




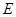 的中心在原点
的中心在原点 ,焦点
,焦点 ,
,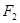 在
在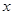 轴上,经过点
轴上,经过点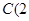 ,
,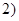 ,且抛物线
,且抛物线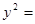
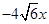 的焦点为
的焦点为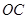 的直线
的直线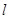 与椭圆
与椭圆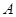 ,
,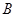 两点,当以
两点,当以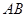 为直径的圆
为直径的圆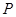 与
与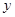 轴相切时,求直线
轴相切时,求直线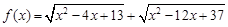 的最小值为 .
的最小值为 .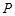 在曲线
在曲线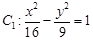 上,点
上,点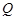 在曲线
在曲线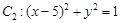 上,点
上,点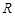 在曲线
在曲线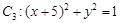 上,则
上,则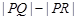 的最大值是 .
的最大值是 .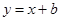 与曲线
与曲线 有公共点,则
有公共点,则 的取值范围是 .
的取值范围是 .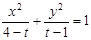 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题: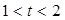 ,则C表是长轴在x轴上的椭圆.
,则C表是长轴在x轴上的椭圆.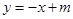 与曲线
与曲线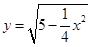 只有一个公共点,则
只有一个公共点,则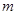 的取值范围是________.
的取值范围是________. 的实轴长是
的实轴长是

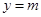 与椭圆
与椭圆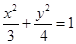 有两个不同的交点,则实数
有两个不同的交点,则实数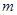 的取值范围是
的取值范围是 。
。