题目内容
已知 为等差数列
为等差数列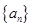 的前
的前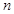 项和,且
项和,且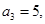
 .
.
(Ⅰ)求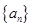 的通项公式;
的通项公式;
(Ⅱ)求数列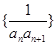 的前
的前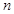 项和
项和 .
.
(Ⅰ)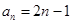 ;(Ⅱ)
;(Ⅱ)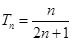 .
.
解析试题分析:(Ⅰ)求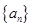 的通项公式,关键是求等差数列
的通项公式,关键是求等差数列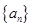 的首项及公差即
的首项及公差即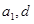 ,由已知可知
,由已知可知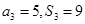 ,即
,即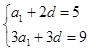 ,解方程组得
,解方程组得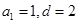 ,有等差数列的通项公式即可写出
,有等差数列的通项公式即可写出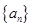 的通项公式;(Ⅱ)求数列
的通项公式;(Ⅱ)求数列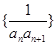 的前
的前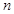 项和
项和 ,首先求出数列
,首先求出数列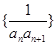 的通项公式,由(Ⅰ)可知
的通项公式,由(Ⅰ)可知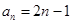 ,从而可得
,从而可得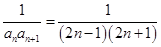 ,分母是等差数列
,分母是等差数列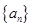 的连续两项的积,符合利用拆项相消法求和,故
的连续两项的积,符合利用拆项相消法求和,故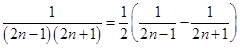 ,即可求出.
,即可求出.
试题解析:(Ⅰ)设等差数列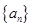 的公差为
的公差为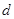 .因为
.因为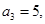
 ,
,
所以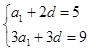 解得
解得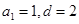 4分
4分
所以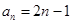 6分
6分
(Ⅱ)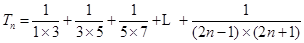
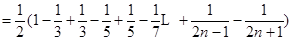
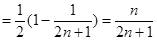 12分
12分
考点:等差数列的通项公式,数列求和.

练习册系列答案
相关题目
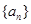 的前
的前 项和为
项和为 ,且
,且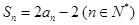 ,数列
,数列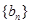 满足
满足 ,且
,且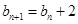 .
. 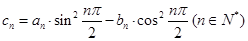 ,求数列
,求数列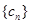 的前
的前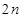 项和
项和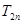 .
. 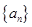 的前
的前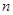 项和记为
项和记为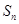 ,
,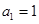 ,
,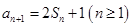 .
.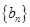 的前
的前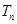 有最大值,且
有最大值,且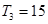 ,又
,又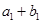 、
、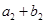 、
、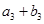 成等比数列,求
成等比数列,求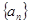 中,
中,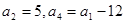 .
.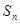 取最大值时求
取最大值时求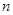 的值.
的值. 的前
的前 项和为
项和为 .且
.且 .
. ,数列
,数列 满足:
满足:

 ,求数列
,求数列 的前
的前 项和
项和 .
.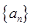 是首项为
是首项为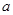 ,公差为
,公差为 的等差数列
的等差数列 ,
, 是其前
是其前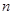 项和.
项和. ,
, ,求数列
,求数列 ,
, ,且
,且 、
、 、
、 成等比数列,证明:
成等比数列,证明: .
.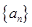 的前
的前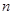 项和为
项和为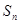 ,公差
,公差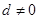 ,
,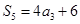 ,且
,且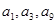 成等比数列.
成等比数列.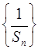 的前
的前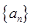 的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=2x+1上,n∈N*.
的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=2x+1上,n∈N*. 为何值时,数列
为何值时,数列 是数列
是数列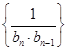 的前
的前 项和,求
项和,求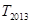 的值.
的值.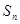 为其前n项和
为其前n项和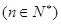 ,且
,且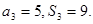
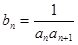 ,求数列
,求数列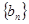 的前
的前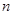 项和
项和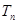 .
.