题目内容
设函数f(x)=a·b,其中向量a=(cos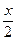 ,sin
,sin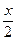 ),(x∈R),向量b=(cosj,sinj)
),(x∈R),向量b=(cosj,sinj)
(Ⅰ)求j的值;
(Ⅱ)若函数y=1+sin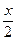 的图象按向量c=(m,n)(| m |<p)平移可得到函数
的图象按向量c=(m,n)(| m |<p)平移可得到函数
y=f(x)的图象,求向量c.
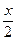 ,sin
,sin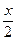 ),(x∈R),向量b=(cosj,sinj)
),(x∈R),向量b=(cosj,sinj)(Ⅰ)求j的值;
(Ⅱ)若函数y=1+sin
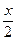 的图象按向量c=(m,n)(| m |<p)平移可得到函数
的图象按向量c=(m,n)(| m |<p)平移可得到函数y=f(x)的图象,求向量c.
(1)j=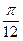 (2)=(-
(2)=(-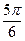 ,-1)
,-1)
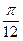 (2)=(-
(2)=(-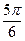 ,-1)
,-1)(Ⅰ)f(x)=a×b=cos
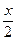 cosj+sin
cosj+sin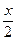 sinj=cos(
sinj=cos(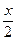 -j),∵f(x)的图象关于x=
-j),∵f(x)的图象关于x=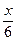 对称,
对称,∴
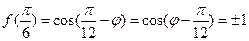 ,………………………3分
,………………………3分∴
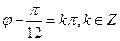 ,又|j|<,∴j=. ………………………5分
,又|j|<,∴j=. ………………………5分(Ⅱ)f(x)=cos(-)=sin(+)=sin(x+),
由y=1+ sin平移到
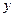 =sin(x+),只需向左平移单位,再向下平移1个单位,
=sin(x+),只需向左平移单位,再向下平移1个单位,考虑到函数的周期为
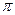 ,且=(m,n)(| m |<π),………………………8分
,且=(m,n)(| m |<π),………………………8分∴
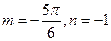 ,即=(-,-1).………………………10分
,即=(-,-1).………………………10分另解:f(x)=cos(-)=sin(+)=sin(x+),
由
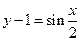 平移到
平移到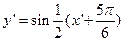 ,只要
,只要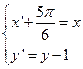 即
即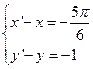 ,
,∴=(-,-1).………………………10分
【总结点评】本题是一道三角函数与平面向量相结合的综合问题,既考查了三角函数的变形以及三角函数的图象与性质,又考查了运用平面向量进行图象平移的知识.

练习册系列答案
相关题目
 ,
, ,(Ⅰ)如果函数
,(Ⅰ)如果函数 的图像是由函数
的图像是由函数 得到,求函数
得到,求函数 解析式;
解析式; ,求
,求 上的值域.
上的值域.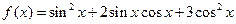 ,
,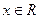 .求:
.求: 函数
函数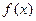 的最大值及取得最大值的自变量
的最大值及取得最大值的自变量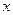 的集合;
的集合;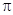 ,且图象关于直线
,且图象关于直线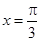 对称的是
对称的是 



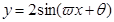 为偶函数(
为偶函数(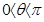 )其图像与直线y=2的某两个交点横坐标为
)其图像与直线y=2的某两个交点横坐标为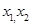 ,若
,若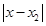 的最小值为π,则( )
的最小值为π,则( )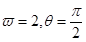
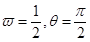
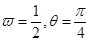
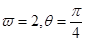
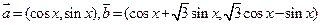 ,
,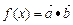 .
.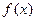 的解析式及周期
的解析式及周期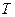 ;
; 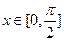 时,
时, 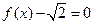 ,求
,求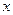 的值.
的值.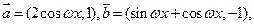
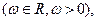 设函数
设函数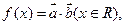 若
若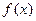 的最小正周期为
的最小正周期为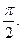 (1)求
(1)求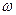 的值;(2)求
的值;(2)求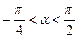 ),则α∈( )
),则α∈( )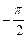 ,
,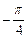 ) B(
) B(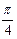 ) D.(
) D.(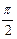 )
) 的终边落在直线
的终边落在直线 上,求
上,求 和
和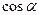 的值.
的值.