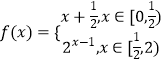Question

【题目】给出下列四种说法：
①函数y=ax（a＞0且a≠1）与函数y=logaax（a＞0且a≠1）的定义域相同；
②函数y=x3与y=3x的值域相同；
③函数y= + 与y= 都是奇函数；
④函数y=（x﹣1）2与y=2x﹣1在区间[0，+∞）上都是增函数．
其中正确的序号是（把你认为正确叙述的序号都填上）．

Answer 1

【答案】①③
【解析】解：①中两函数的定义域均为R，故①正确；
②中函数y=x3的值域为R，y=3x的值域（0，+∞），故②错误；
③中 ，所以f（﹣x）=﹣f（﹣x），为奇函数，
而 ，y= 是奇函数，y=2x+2﹣x+2是偶函数，所以y= 是奇函数，故③正确；
④函数y=（x﹣1）2在[1，+∞）上单增，故④错误．
所以答案是：①③
【考点精析】根据题目的已知条件，利用命题的真假判断与应用的相关知识可以得到问题的答案，需要掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系．