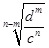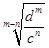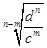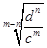题目内容
已知数列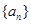 的各项均为正数,
的各项均为正数,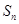 为其前
为其前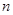 项和,对于任意的
项和,对于任意的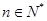 ,满足关系式
,满足关系式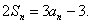
(1)求数列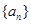 的通项公式;
的通项公式;
(2)设数列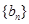 的通项公式是
的通项公式是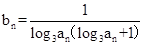 ,前
,前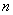 项和为
项和为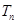 ,求证:对于任意的正整数
,求证:对于任意的正整数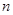 ,总有
,总有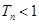 .
.
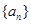 的各项均为正数,
的各项均为正数,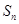 为其前
为其前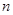 项和,对于任意的
项和,对于任意的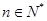 ,满足关系式
,满足关系式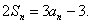
(1)求数列
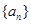 的通项公式;
的通项公式;(2)设数列
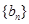 的通项公式是
的通项公式是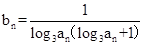 ,前
,前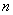 项和为
项和为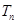 ,求证:对于任意的正整数
,求证:对于任意的正整数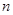 ,总有
,总有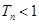 .
.(1)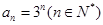 ;(2)详见解析.
;(2)详见解析.
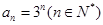 ;(2)详见解析.
;(2)详见解析.试题分析:(1)仿写
 成
成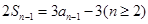 ,两式相减可得数列
,两式相减可得数列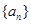 是一个等比数列,求出其通项;(2)
是一个等比数列,求出其通项;(2)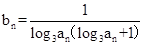 化简为
化简为 ,结合其特点利用裂项相消法求和.
,结合其特点利用裂项相消法求和.试题解析:
(1)由已知得

故

即

故数列
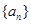 为等比数列,且
为等比数列,且
又当
 时,
时,
所以
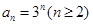 而
而 亦适合上式
亦适合上式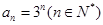 6分
6分(2)

所以
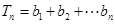

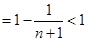 . 12分
. 12分
练习册系列答案
相关题目
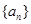 满足
满足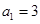 ,
,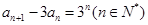 ,数列
,数列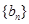 满足
满足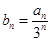 .
.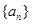 的前n项和
的前n项和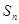 .
.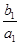 +
+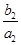 +…+
+…+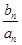 =1-
=1-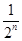 ,n∈N*,求{bn}的前n项和Tn.
,n∈N*,求{bn}的前n项和Tn.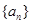 、
、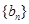 满足
满足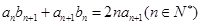 .
.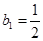 时,求数列
时,求数列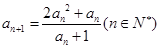 ,
,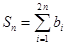 ,求证:
,求证: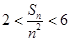 .
.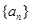 满足:
满足: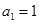 ,
,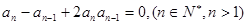
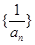 是等差数列并求
是等差数列并求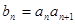 ,求证:
,求证: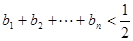 .
.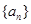 的前
的前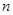 项和为
项和为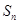 .若
.若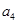 是
是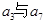 的等比中项,
的等比中项, 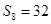 ,则
,则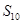 =( ).
=( ). 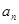 }满足
}满足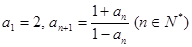 ,则
,则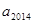 的值为 .
的值为 .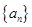 为等差数列,若
为等差数列,若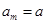 ,
,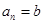 (
(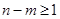 ,
,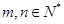 ),则
),则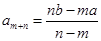 .类比上述结论,对于等比数列
.类比上述结论,对于等比数列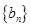 (
(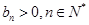 ),若
),若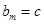 ,
,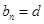 (
(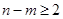 ,
,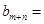 ( )
( )