题目内容
8.已知f(x)=sin(2015x+$\frac{π}{6}$)+cos(2015x-$\frac{π}{3}$)的最大值为A,若存在实数x1、x2,使得对任意实数x总有f(x1)≤f(x)≤f(x2)成立,则A|x1-x2|的最小值为( )| A. | $\frac{π}{2015}$ | B. | $\frac{2π}{2015}$ | C. | $\frac{4π}{2015}$ | D. | $\frac{π}{4030}$ |
分析 根据题意,利用三角恒等变换化简函数f(x)的解析式,
再利用正弦函数的周期性和最值,即可求出 A|x1-x2|的最小值.
解答 解:f(x)=sin(2015x+$\frac{π}{6}$)+cos(2015x-$\frac{π}{3}$)
=sin2015xcos$\frac{π}{6}$+cos2015xsin$\frac{π}{6}$+cos2015xcos$\frac{π}{3}$+sin2015xsin$\frac{π}{3}$
=$\frac{\sqrt{3}}{2}$sin2015x+$\frac{1}{2}$cos2015x+$\frac{1}{2}$cos2015x+$\frac{\sqrt{3}}{2}$sin2015x
=$\sqrt{3}$sin2015x+cos2015x
=2($\frac{\sqrt{3}}{2}$sin2015x+$\frac{1}{2}$cos2015x)
=2sin(2015x+$\frac{π}{6}$),
∴f(x) 的最大值为A=2;
由题意得,|x1-x2|的最小值为$\frac{T}{2}$=$\frac{π}{2015}$,
∴A|x1-x2|的最小值为$\frac{2π}{2015}$.
故选:B.
点评 本题考查了三角函数的恒等变换以及正弦、余弦函数的周期性和最值问题,是基础题目.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
20.设函数f(x)=alnx+bx2,若函数f(x)的图象在点(1,1)处的切线与y轴垂直,则实数a+b=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | -1 |
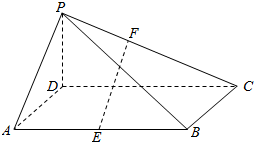 在如图所示的四棱锥中,底面ABCD是平行四边形,AB=4,BC=2,∠BCD=60°,且PD⊥底面ABCD,点E是AB的中点,点F是PC上一点.
在如图所示的四棱锥中,底面ABCD是平行四边形,AB=4,BC=2,∠BCD=60°,且PD⊥底面ABCD,点E是AB的中点,点F是PC上一点.