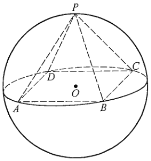
题目内容
【题目】房屋的天花板上点![]() 处有一光源,
处有一光源,![]() 在地面上的射影为
在地面上的射影为![]() ,在地面上放置正棱锥
,在地面上放置正棱锥![]() ,底面
,底面![]() 接触地面.已知正四棱锥
接触地面.已知正四棱锥![]() 的高为
的高为![]() ,底面
,底面![]() 的边长为
的边长为![]() ,
,![]() 与正方形
与正方形![]() 的中心
的中心![]() 的距离为
的距离为![]() ,又
,又![]() 长为
长为![]() ,则棱锥影子(不包括底面
,则棱锥影子(不包括底面![]() )的面积的最大值为________.
)的面积的最大值为________.
【答案】![]()
【解析】
作出图形,利用相似三角形求出影子的高![]() ,由此可得出棱锥影子(不包括底面
,由此可得出棱锥影子(不包括底面![]() )的面积为
)的面积为![]() ,欲使得棱锥影子(不包括底面
,欲使得棱锥影子(不包括底面![]() )的面积最大,则
)的面积最大,则![]() 最大,即
最大,即![]() 且点
且点![]() 在直线
在直线![]() 上,最后利用三角形的面积公式计算出棱锥的影子(不包括底面
上,最后利用三角形的面积公式计算出棱锥的影子(不包括底面![]() )的面积即可.
)的面积即可.
如下图所示:

设影子![]() ,由
,由![]() ,得
,得![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以,棱锥的影子(不包括底面![]() )的面积为
)的面积为![]() ,
,
欲使得棱锥影子(不包括底面![]() )的面积最大,则
)的面积最大,则![]() 的面积取最大值,此时
的面积取最大值,此时![]() 且点
且点![]() 在直线
在直线![]() 上,
上,
所以,棱锥的影子(不包括底面![]() )的面积的最大值为
)的面积的最大值为![]() .
.
故答案为:![]() .
.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目