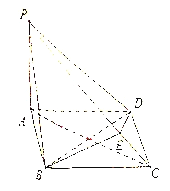
题目内容

【题目】已知为棱长的正方体， 为棱的中点.

（1）求三棱锥的体积；

（2）求证： 平面.

【答案】（1）;（2）见解析.

【解析】试题分析：（1）高为ED,再根据锥体体积公式计算体积（2）连接交于点，根据三角形中位线性质得，再根据线面平行判定定理得结论

试题解析：（1）体积

（2）连接交于点，则为的中位线，即，

又面， 面，得到 平面.

【题型】解答题
【结束】
18

【题目】已知抛物线： 的焦点为圆的圆心.

（1）求抛物线的标准方程；

（2）若斜率的直线过抛物线的焦点与抛物线相交于两点，求弦长.

【答案】（1）;（2）8.

【解析】试题分析：（1）先求圆心得焦点,根据焦点得抛物线方程（2）先根据点斜式得直线方程,与抛物线联立方程组,利用韦达定理以及弦长公式得弦长.

试题解析：（1）圆的标准方程为，圆心坐标为，

即焦点坐标为，得到抛物线的方程：

（2）直线： ，联立，得到

弦长

练习册系列答案
相关题目

【题目】若f(x)是定义在(0，＋∞)上的增函数，且对一切x，y>0，满足．

(1)求f(1)的值；

(2)若f(6)＝1，解不等式f(x＋3)－f()<2.

【题目】在△ABC中，a，b，c分别是三内角A，B，C所对应的三边，已知b2+c2=a2+bc
（1）求角A的大小；
（2）若 ，试判断△ABC的形状．

【题目】（选修4﹣4：坐标系与参数方程）
已知曲线C1的参数方程为 （t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=2sinθ．
（1）把C1的参数方程化为极坐标方程；
（2）求C1与C2交点的极坐标（ρ≥0，0≤θ＜2π）

【题目】（本题满分12分）

一个盒子中装有4张卡片，每张卡片上写有1个数字，数字分别是1、2、3、4，现从盒子中随机抽取卡片.

(Ⅰ)若一次从中随机抽取3张卡片，求3张卡片上数字之和大于或等于7的概率；

(Ⅱ)若第一次随机抽取1张卡片，放回后再随机抽取1张卡片，求两次抽取的卡片中至少一次抽到数字2的概率.

【题目】已知函数在点处的切线方程为.

（1）求函数的解析式；

（2）求函数的单调区间和极值.

【答案】（1）;（2）见解析.

【解析】试题分析：（1）根据导数几何意义得，再与联立方程组解得， （2）先函数导数,再求导函数零点,列表分析导函数符号变化规律,进而确定单调区间和极值

试题解析：（1），切线为，即斜率，纵坐标

即， ，解得，

解析式

（2） ，定义域为

得到在单增，在单减，在单增

极大值，极小值.

【题型】解答题
【结束】
20

【题目】如图：在四棱锥中，底面为菱形，且， 底面，

， ， 是上点，且平面.

（1）求证： ；（2）求三棱锥的体积.

【题目】在框图中，设x=2，并在输入框中输入n=4；ai=i（i=0，1，2，3，4）．则此程序执行后输出的S值为（ ）

A.26
B.49
C.52
D.98

【题目】已知椭圆： 的两个焦点分别为， ，且点在椭圆上.

（1）求椭圆的标准方程；

（2）设椭圆的左顶点为，过点的直线与椭圆相交于异于的不同两点，求的面积的最大值.

【题目】已知{an}为等差数列，前n项和为Sn（n∈N*），{bn}是首项为2的等比数列，且公比大于0，b2+b3=12，b3=a4-2a1，S11=11b4．

（Ⅰ）求{an}和{bn}的通项公式；

（Ⅱ）求数列{a2nbn}的前n项和（n∈N*）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网