题目内容
【题目】设数列{an}的前n项和为Sn ， a1=1，an= 
+2（n﹣1）（n∈N*）．
（1）求证：数列{an}为等差数列，并分别写出an和Sn关于n的表达式；
（2）设数列 
的前n项和为Tn ， 证明： 
．
【答案】
（1）证明：由an= 
+2（n﹣1），得Sn=nan﹣2n（n﹣1）（n∈N*）．
当n≥2时，an=Sn﹣Sn﹣1=nan﹣（n﹣1）an﹣1﹣4（n﹣1），即an﹣an﹣1=4，
∴数列{an}是以a1=1为首项，4为公差的等差数列．
于是，an=4n﹣3，Sn= 
=2n2﹣n（n∈N*）
（2）证明：Tn= 
+ 
+ 
+…+ 
= 
+ 
+ 
+…+ 
．
= 
[（1﹣ 
）+（ ﹣ 
）+（ ﹣ 
）+…+（ 
﹣ 
）]
= （1﹣ ）= 
＜ 
=
又由题意知Tn单调递增，故Tn≥T1= ，
于是， ≤Tn＜
【解析】（1）由an= +2（n﹣1），得Sn=nan﹣2n（n﹣1）（n∈N*），由此能证明数列{an}为等差数列，并能求出an和Sn关于n的表达式．（2）由 =（ ﹣ ），利用裂项求和法能证明 ≤Tn＜ ．
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系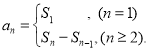
，以及对数列的通项公式的理解，了解如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
练习册系列答案
名校课堂系列答案
相关题目
