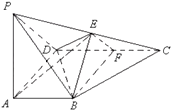
题目内容
【题目】在平面直角坐标平面中,![]() 的两个顶点为
的两个顶点为![]() ,平面内两点
,平面内两点![]() 、
、![]() 同时满足:①
同时满足:①![]() +
+![]() +
+![]() =
=![]() ;②|
;②|![]() |=|
|=|![]() |=|
|=|![]() |;③
|;③![]() ∥
∥![]() .
.
(1)求顶点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,直线
,直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 相交弦分别为
相交弦分别为![]() ,设弦
,设弦![]() 的中点分别为
的中点分别为![]() .求四边形
.求四边形![]() 的面积
的面积![]() 的最小值;
的最小值;
【答案】(1) ![]() ;(2)当
;(2)当![]() ,即
,即![]() 时取等号.
时取等号.
【解析】
(1)由![]() +
+![]() +
+![]() =
=![]() 可得P为△ABC的重心,设A(x,y),则P(
可得P为△ABC的重心,设A(x,y),则P(![]() ),再由|
),再由|![]() |=|
|=|![]() |=|
|=|![]() |,知Q是△ABC的外心,Q在x轴上,再由
|,知Q是△ABC的外心,Q在x轴上,再由![]() ∥
∥![]() ,可得Q(
,可得Q(![]() ),结合|
),结合|![]() |=|
|=|![]() |求得顶点A的轨迹E的方程;
|求得顶点A的轨迹E的方程;
(2)F(![]() ,0)恰为
,0)恰为![]() 的右焦点.当直线l1,l2的斜率存在且不为0时,设直线l1 的方程为my=x﹣
的右焦点.当直线l1,l2的斜率存在且不为0时,设直线l1 的方程为my=x﹣![]() .联立直线方程与椭圆方程,化为关于y的一元二次方程,利用根与系数的关系求得A、B的纵坐标得到和与积,根据焦半径公式得|A1B1|、|A2B2|,代入四边形面积公式再由基本不等式求得四边形A1A2B1B2的面积S的最小值.
.联立直线方程与椭圆方程,化为关于y的一元二次方程,利用根与系数的关系求得A、B的纵坐标得到和与积,根据焦半径公式得|A1B1|、|A2B2|,代入四边形面积公式再由基本不等式求得四边形A1A2B1B2的面积S的最小值.
(1)∵![]() ,由①知
,由①知![]() ,∴
,∴![]() 为
为![]() 的重心,设
的重心,设![]() ,则
,则![]() ,由②知
,由②知![]() 是
是![]() 的外心,∴
的外心,∴![]() 在
在![]() 轴上由③知
轴上由③知![]() ,由
,由![]() ,得
,得![]() ,化简整理得:
,化简整理得:![]() .
.
(2)解:![]() 恰为
恰为![]() 的右焦点,
的右焦点,
①当直线![]() 的斜率存且不为0时,设直线
的斜率存且不为0时,设直线![]() 的方程为
的方程为![]() ,
,
由![]() ,
,
设![]() 则
则![]() ,
,
①根据焦半径公式得![]() ,
,
又![]() ,
,
所以![]() ,同理
,同理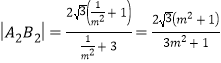 ,
,
则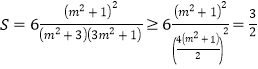 ,
,
当![]() ,即
,即![]() 时取等号.
时取等号.

练习册系列答案
相关题目