题目内容
4.函数f(x)=2x+a•2-x是偶函数,则a的值为1_.分析 根据函数奇偶性的定义进行求解即可.
解答 解:∵f(x)=2x+a•2-x是偶函数,
∴f(-x)=f(x),
即f(-x)=2-x+a•2x=2x+a•2-x,
则(2-x-2x)=a(2-x-2x),
即a=1,
故答案为:1
点评 本题主要考查函数奇偶性的应用,根据条件建立方程关系是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知函数y=sin2x,则函数的周期为( )
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
19.如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2012}$的值的程序框图,其中判断框内应填入的是( )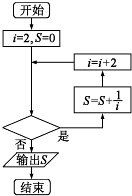

| A. | i≤2012 | B. | i>2012 | C. | i≤1006 | D. | i>1006 |
14.对某种灯泡中随机地抽取200个样品进行使用寿命调查,结果如下:
规定:使用寿命大于或等于500天的灯泡是优等品,小于300天是次品,其余的是正品.
(Ⅰ)根据频率分布表中的数据,求得x=30,y=0.15;
(Ⅱ)某人从灯泡样品中随机地购买了n(n∈N*)个,如果这n个灯泡的等级分布情况恰好与从这200个样品中按三个等级分层抽样所得的结果相同,则n的最小值为4.
| 寿命(天) | 频数 | 频率 |
| [100,200) | 20 | 0.10 |
| [200,300) | 30 | y |
| [300,400) | 70 | 0.35 |
| [400,500) | x | 0.15 |
| [500,600) | 50 | 0.25 |
| 合计 | 200 | 1 |
(Ⅰ)根据频率分布表中的数据,求得x=30,y=0.15;
(Ⅱ)某人从灯泡样品中随机地购买了n(n∈N*)个,如果这n个灯泡的等级分布情况恰好与从这200个样品中按三个等级分层抽样所得的结果相同,则n的最小值为4.
 已知an=$\frac{n}{2015}$,把数列{an}中的各项排成如图所示的三角形形状,记A(m,n)表示第m行的第n个数,则A(9,13)表示的数为$\frac{77}{2015}$.
已知an=$\frac{n}{2015}$,把数列{an}中的各项排成如图所示的三角形形状,记A(m,n)表示第m行的第n个数,则A(9,13)表示的数为$\frac{77}{2015}$.