题目内容
(本小题满分12分)设等比数列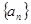 的公比为
的公比为 ,前n项和
,前n项和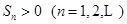 。
。
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)设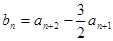 ,记
,记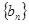 的前n项和为
的前n项和为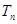 ,试比较
,试比较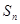 与
与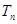 的大小。
的大小。
(Ⅰ)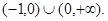 (Ⅱ)当
(Ⅱ)当 或
或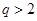 时,
时,
当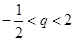 ,
,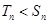 ;当
;当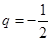 或
或 =2时,
=2时,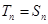
解析试题分析:(Ⅰ)因为 是等比数列,
是等比数列,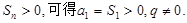
当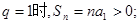
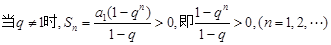
上式等价于不等式组: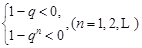 ① 或
① 或 ②
②
解①式得q>1;解②,由于n可为奇数、可为偶数,得-1<q<1.
综上,q的取值范围是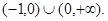 ……6分
……6分
(Ⅱ)由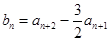 得
得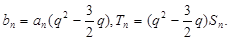
于是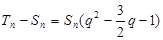
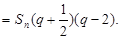
又∵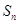 >0且-1<
>0且-1< <0或
<0或 >0
>0
当 或
或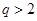 时,
时,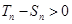 即
即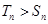
当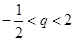 且
且 ≠0时,
≠0时,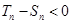 即
即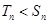
当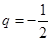 或
或 =2时,
=2时,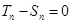 即
即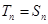 . ……12分
. ……12分
考点:本小题主要考查等比数列前n项和公式的应用和作差法比较大小,考查学生对公式的应用和分类讨论思想的应用.
点评:应用等比数列的前n项和公式时,要注意公比是否为1,必要时要分情况讨论;比较两个数或两个式子的大小时,常用的方法是作差法或作商法.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
已知函数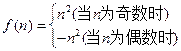 且an=f(n)+f(n+1),则a1+a2+a3+…+a100等于( )
且an=f(n)+f(n+1),则a1+a2+a3+…+a100等于( )
| A.0 |
| B.100 |
| C.-100 |
| D.10200 |
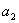 ,
,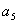 是方程
是方程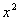
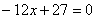 的两根, 数列
的两根, 数列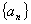 是公差为正的等差数列,数列
是公差为正的等差数列,数列 的前
的前 项和为
项和为 ,且
,且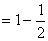
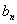
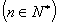 .
.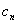 =
=
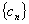 的前
的前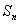 .
. ,已知
,已知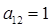 ,
,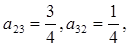 又设第一行数列的公差为
又设第一行数列的公差为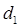 .
.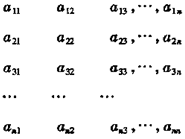
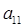 ,
,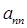 的表达式,并求
的表达式,并求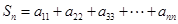 的值.
的值. 满足
满足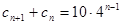 ,
, ,数列
,数列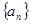 满足
满足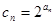
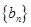 满足
满足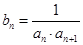 ,
,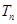 为数列
为数列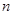 项和.求
项和.求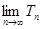 ;(5分)
;(5分)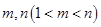 ,使得
,使得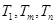 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有 的值;若不存在,请说明理由.(6分)
的值;若不存在,请说明理由.(6分)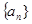 的前n项和
的前n项和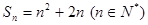 .
.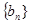 是等比数列,公比为
是等比数列,公比为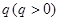 ,且满足
,且满足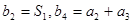 ,求数列
,求数列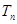 .
.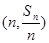 在直线
在直线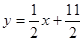 上.数列{bn}满足
上.数列{bn}满足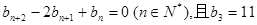 ,前9项和为153.
,前9项和为153.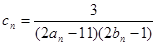 ,数列{cn}的前n和为Tn,求使不等式
,数列{cn}的前n和为Tn,求使不等式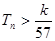 对一切
对一切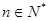 都成立的最大正整数k的值.
都成立的最大正整数k的值.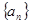 是公差不为零的等差数列,
是公差不为零的等差数列,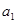 =1,且
=1,且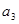 ,
,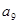 成等比数列.
成等比数列.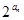 }的前n项和
}的前n项和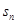 .
.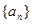 满足:
满足: 
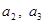 ;
; 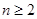 时,求
时,求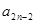 与
与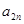 的关系式,并求数列
的关系式,并求数列