题目内容
等比数列 满足
满足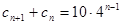 ,
, ,数列
,数列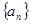 满足
满足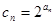
(1)求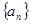 的通项公式;(5分)
的通项公式;(5分)
(2)数列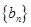 满足
满足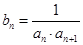 ,
,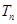 为数列
为数列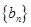 的前
的前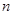 项和.求
项和.求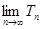 ;(5分)
;(5分)
(3)是否存在正整数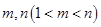 ,使得
,使得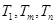 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有 的值;若不存在,请说明理由.(6分)
的值;若不存在,请说明理由.(6分)
(1)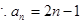 ;(2)
;(2)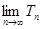 =
=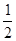
(3)当且仅当 ,
,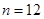 时,
时,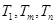 成等比数列。
成等比数列。
解析试题分析:(1)解: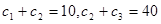 ,所以公比
,所以公比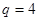 2分
2分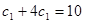 计算出
计算出 3分
3分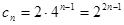 4分
4分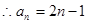 5分
5分
(2)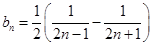 6分
6分
于是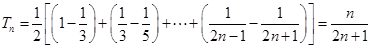 8分
8分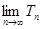 =
=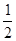 10分
10分
(3)假设否存在正整数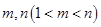 ,使得
,使得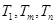 成等比数列,则
成等比数列,则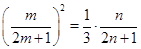 , 12分
, 12分
可得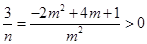 ,
,
由分子为正,解得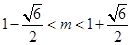 ,
,
由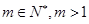 ,得
,得 ,此时
,此时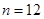 ,
,
当且仅当 ,
,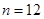 时,
时,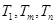 成等比数列。 16分
成等比数列。 16分
说明:只有结论, ,
,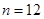 时,
时,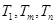 成等比数列。若学生没有说明理由,则只能得 13分
成等比数列。若学生没有说明理由,则只能得 13分
考点:本题主要考查等比数列的概念、通项公式,裂项相消法求和,不等式解法。
点评:综合题,本题综合考查等比数列知识、数列的求和、不等式解法,对考查考生灵活运用数学知识的能力起到了很好的作用。

练习册系列答案
相关题目
已知数列{an}的前n项和为Sn,对任意的n∈N*有Sn=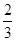 an-
an-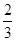 ,且1<Sk<12,则k的值为( )
,且1<Sk<12,则k的值为( )
| A.2 | B.2或4 | C.3或4 | D.6 |
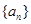 为等差数列,
为等差数列,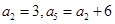 ,数列
,数列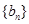 满足
满足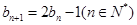 ,且
,且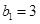 .(1)求通项公式
.(1)求通项公式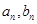 ;(2)设数列
;(2)设数列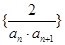 的前
的前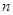 项和为
项和为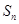 ,试比较
,试比较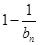 的大小.
的大小.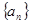 中,
中, 为常数,
为常数, ,且
,且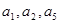 成公比不等于1的等比数列.
成公比不等于1的等比数列.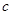 的值;
的值;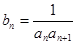 ,求数列
,求数列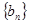 的前
的前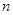 项和
项和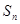 。
。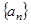 前
前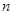 项和为
项和为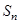 ,首项为
,首项为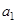 ,且
,且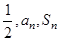 等差数列.
等差数列.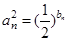 ,设
,设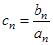 ,求数列
,求数列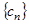 的前
的前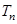 .
.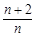 Sn(n=1,2,3…).
Sn(n=1,2,3…).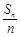 }是等比数列.
}是等比数列.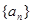 是等比数列,
是等比数列,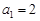 ,且
,且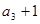 是
是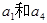 的等差中项.
的等差中项.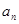 ;
;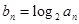 ,求数列
,求数列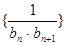 的前n项和
的前n项和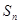 .
.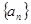 的公比为
的公比为 ,前n项和
,前n项和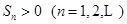 。
。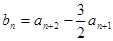 ,记
,记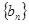 的前n项和为
的前n项和为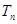 ,试比较
,试比较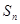 与
与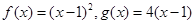 ,数列
,数列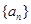 满足
满足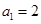 ,且
,且 .
.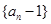 是否是等比数列?(5分)
是否是等比数列?(5分)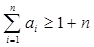 .(5分)
.(5分)