题目内容
(本小题满分14分)
已知数列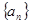 是公差不为零的等差数列,
是公差不为零的等差数列,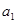 =1,且
=1,且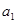 ,
,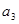 ,
,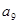 成等比数列.
成等比数列.
(Ⅰ)求数列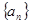 的通项公式; (Ⅱ)求数列{
的通项公式; (Ⅱ)求数列{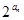 }的前n项和
}的前n项和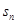 .
.
(Ⅰ)an=1+(n-1)×1=n.
(Ⅱ)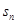 =2+22+23+…+2n=
=2+22+23+…+2n=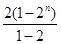 =2n+1-2.
=2n+1-2.
解析试题分析:(I)根据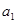 ,
,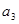 ,
,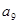 成等比数列.可建立关于d的方程,求出d的值.从而得到
成等比数列.可建立关于d的方程,求出d的值.从而得到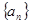 的通项公式;
的通项公式;
(II)在(I)的基础上,可知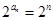 ,因而可知此数列为等比数列,利用等比数列的前n项和公式求解即可.
,因而可知此数列为等比数列,利用等比数列的前n项和公式求解即可.
(Ⅰ)由题设知公差d≠0,
由a1=1,a1,a3,a9成等比数列得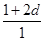 =
=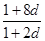 ,解得d=1,d=0(舍去), ..........................4分
,解得d=1,d=0(舍去), ..........................4分
故{an}的通项an=1+(n-1)×1=n. ...7分
(Ⅱ)由(Ⅰ)知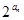 =2n,由等比数列前n项和公式得
=2n,由等比数列前n项和公式得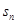 =2+22+23+…+2n=
=2+22+23+…+2n=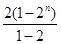 =2n+1-2. .......14分
=2n+1-2. .......14分
考点:等差数列的通项公式及等比数列的前n项和公式.
点评:本小题用到等比数列前n项和公式: 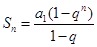 .
.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
已知函数f(x)=xa的图象过点(4,2),令an=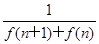 ,n∈N*.记数列{an}的前n项和为Sn,则S2 013=( )
,n∈N*.记数列{an}的前n项和为Sn,则S2 013=( )
A.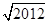 -1 -1 | B.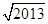 -1 -1 |
C. -1 -1 | D. +1 +1 |
 的首项
的首项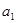 为a
为a ,设数列的前n项和为
,设数列的前n项和为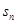 ,且
,且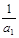 ,
,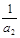 ,
,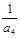 成等比数列.
成等比数列.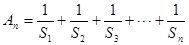 ,
,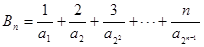 ,当
,当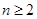 时,计算
时,计算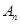 与
与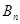 ,并比较
,并比较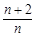 Sn(n=1,2,3…).
Sn(n=1,2,3…).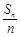 }是等比数列.
}是等比数列.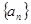 的公比为
的公比为 ,前n项和
,前n项和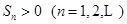 。
。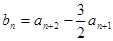 ,记
,记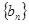 的前n项和为
的前n项和为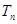 ,试比较
,试比较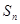 与
与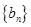
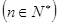 是递增的等比数列,且
是递增的等比数列,且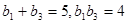 .
.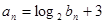 ,求证数列
,求证数列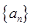 是等差数列;
是等差数列;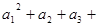 ……
……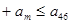 ,求
,求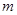 的最大值.
的最大值. 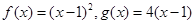 ,数列
,数列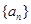 满足
满足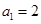 ,且
,且 .
.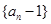 是否是等比数列?(5分)
是否是等比数列?(5分)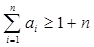 .(5分)
.(5分) 的前
的前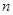 项和
项和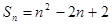 ,求通项公式
,求通项公式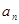 ;
;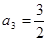 ,
,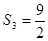 ,求通项公式
,求通项公式 ,
,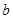 ,
,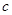 成等比数列,其公比为3,如果
成等比数列,其公比为3,如果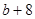 ,
,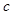 成等差数列,求这三个数.
成等差数列,求这三个数.