题目内容
已知函数f(x)是定义在(0,+∞)上的单调函数,若对任意x∈(0,+∞),都有f(f(x)-
)=2,则f(
)的值是( )
)=2,则f()的值是( )| A．5 | B．6 | C．7 | D．8 |
B
【思路点拨】解答本题的关键是从条件中得出f(x)-是一个常数,从而令f(x)=+k(k为常数),则f(x)可求.
解：由题意知f(x)-为常数,令f(x)-=k(k为常数),
则f(x)=+k,由f(f(x)-)=2得f(k)=2.
又f(k)=
+k=2,∴k=1,即f(x)=+1,
∴f()=6.
是一个常数,从而令f(x)=+k(k为常数),则f(x)可求.解：由题意知f(x)-
为常数,令f(x)-=k(k为常数),则f(x)=
+k,由f(f(x)-)=2得f(k)=2.又f(k)=
+k=2,∴k=1,即f(x)=+1,∴f(
)=6.
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
(单位:元)与上市时间
(单位:天)的数据如下: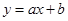
；②
；③
．
<-1.
函数f(x) =max{|x+1|，|x-2|}(x∈R)的最小值是（ ）
，若a，b，c互不相等，且
，则
的取值范围为（ ）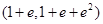
是集合M到集合N的映射, 若N="{1,2}," 则M不可能是 （ ）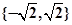
的定义域和值域都是
，其对应关系如下表所示，则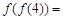
．
(x≠0),那么f(
)等于( )