题目内容
19.已知实数x,y满足不等式组$\left\{\begin{array}{l}{0≤x≤2}\\{x+y≥3}\\{x-y≥-1}\end{array}\right.$,其表示的区域的面积是1.分析 先画出满足条件的平面区域,求出A、B、C的坐标,从而求出三角形的面积即可.
解答 解:画出满足条件的平面区域,如图示: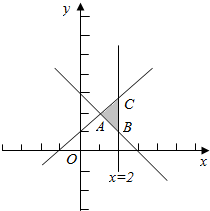 ,
,
由$\left\{\begin{array}{l}{x=2}\\{x+y=3}\end{array}\right.$,解得B(2,1),
由$\left\{\begin{array}{l}{x=2}\\{x-y=-1}\end{array}\right.$,解得C(2,3),
由$\left\{\begin{array}{l}{x+y=3}\\{x-y=-1}\end{array}\right.$,解得A(1,2),
∴S阴影=$\frac{1}{2}$×2×1=1,
故答案为:1.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目