题目内容
18.已知曲线f(x)=$\frac{1}{3}$ax3-4lnx在点(1,f(1))处的切线l与x轴的交点为($\frac{4}{3}$,0).(1)求f(x)的极小值;
(2)求证:对任意x∈(0,+∞),$\frac{{x}^{4}}{6}+\frac{2}{e}$>$\frac{xf(x)}{4}+\frac{x}{{e}^{x}}$(e为自然对数的底数).
分析 (1)求出原函数的导函数,求得函数在点(1,f(1))处的切线l的方程,由切线l与x轴的交点为($\frac{4}{3}$,0),求得a值,则切线方程可求,进一步求出原函数的极小值点,得到f(x)的极小值;
(2)把f(x)的解析式代入$\frac{{x}^{4}}{6}+\frac{2}{e}$>$\frac{xf(x)}{4}+\frac{x}{{e}^{x}}$,转化为证$\frac{x}{{e}^{x}}-\frac{2}{e}<xlnx$,分别构造函数g(x)=xlnx,x∈(0,+∞),h(x)=$\frac{x}{{e}^{x}}-\frac{2}{e}$(0,+∞),然后利用导数分别求出它们的最值得到要证明的结论.
解答 (1)解:由f(x)=$\frac{1}{3}$ax3-4lnx,得f′(x)=$a{x}^{2}-\frac{4}{x}$,
∴f′(1)=a-4,又f(1)=$\frac{a}{3}$,
∴曲线f(x)=$\frac{1}{3}$ax3-4lnx在点(1,f(1))处的切线方程为y-$\frac{a}{3}=(a-4)(x-1)$,
取y=0,得$x=\frac{2(a-6)}{3(a-4)}=\frac{4}{3}$,解得a=2.
∴f′(x)=$2{x}^{2}-\frac{4}{x}=\frac{2{x}^{3}-4}{x}$(x>0),
当x∈(0,$\root{3}{2}$)时,f′(x)<0;当x∈($\root{3}{2}$,+∞)时,f′(x)>0,
则f(x)在(0,$\root{3}{2}$)上为减函数,在x($\root{3}{2}$,+∞)上为增函数,
∴f(x)的极小值为$f(\root{3}{2})$=$\frac{4}{3}-4ln\root{3}{2}=\frac{4}{3}(1-ln2)$;
(2)证明:f(x)=$\frac{2}{3}$x3-4lnx,
要证$\frac{{x}^{4}}{6}+\frac{2}{e}$>$\frac{xf(x)}{4}+\frac{x}{{e}^{x}}$,需要证$\frac{{x}^{4}}{6}+\frac{2}{e}>\frac{x•\frac{2}{3}{x}^{3}-4lnx}{4}+\frac{x}{{e}^{x}}$,
即证$\frac{x}{{e}^{x}}-\frac{2}{e}<xlnx$.
令g(x)=xlnx,x∈(0,+∞),
则g′(x)=lnx+1,
由g′(x)<0,得0$<x<\frac{1}{e}$;由g′(x)>0,得$x>\frac{1}{e}$.
∴当x=$\frac{1}{e}$时取得最小值,最小值为g($\frac{1}{e}$)=-$\frac{1}{e}$,
由h(x)=$\frac{x}{{e}^{x}}-\frac{2}{e}$,可得h′(x)=$\frac{1-x}{{e}^{x}}$.
∴当x∈(0,1),h′(x)>0,h(x)单调递增,
当x∈(1,+∞),h′(x)<0,h(x)单调递减.
函数h(x)(x>0)在x=1时取得最大值,
又h(1)=-$\frac{1}{e}$,∴h(x)$<-\frac{1}{e}$.
∴任意x∈(0,+∞),$\frac{{x}^{4}}{6}+\frac{2}{e}$>$\frac{xf(x)}{4}+\frac{x}{{e}^{x}}$.
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查函数极值的求法,考查了数学转化思想方法,是中档题.

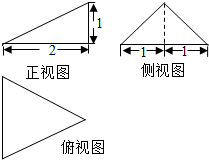 某三棱锥的三视图如图所示,则该三棱锥的4个面中,直角三角形的个数是1个,它的表面积是21.
某三棱锥的三视图如图所示,则该三棱锥的4个面中,直角三角形的个数是1个,它的表面积是21.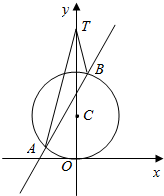 如图,已知圆C的圆心在y轴的正半轴上,且与x轴相切,圆C与直线y=kx+3相交于A,B两点.当$k=\sqrt{3}$时,$|AB|=\sqrt{15}$.
如图,已知圆C的圆心在y轴的正半轴上,且与x轴相切,圆C与直线y=kx+3相交于A,B两点.当$k=\sqrt{3}$时,$|AB|=\sqrt{15}$.