题目内容
对于函数 f(x)=x3+ax2-x+1的极值情况,4位同学有下列说法:甲:该函数必有2个极值;乙:该函数的极大值必大于1;丙:该函数的极小值必小于1;丁:方程 f(x)=0一定有三个不等的实数根.这四种说法中,正确的个数是( )
| A.1个 | B.2个 | C.3个 | D.4个 |
C
解:由题意,f’(x)=3x2+2ax-1,∴△=4a2+12>0,
所以故该函数必有2个极值点x1,x2,x1x2=-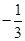 <0
<0
不妨设x1<0,x2>0,易知在x=x1处取得极大值,在x=x2处取得极小值,而f(0)=1,故极大值必大于1,极小值小于1,所以甲、乙、丙三人的说法正确
故选C
所以故该函数必有2个极值点x1,x2,x1x2=-
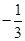 <0
<0不妨设x1<0,x2>0,易知在x=x1处取得极大值,在x=x2处取得极小值,而f(0)=1,故极大值必大于1,极小值小于1,所以甲、乙、丙三人的说法正确
故选C

练习册系列答案
相关题目
 吨,运费为4万元/次,一年的总存储费用为
吨,运费为4万元/次,一年的总存储费用为 万元,要使一年的总运费与总存储费用之和最小,则
万元,要使一年的总运费与总存储费用之和最小,则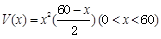 ,则当箱子的容积最大时,箱子底面边长为_________
,则当箱子的容积最大时,箱子底面边长为_________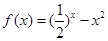 的零点个数是____
的零点个数是____ ,满足
,满足 且
且 ,则
,则 的值为 ▲ .
的值为 ▲ .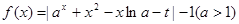 有三个零点,则
有三个零点,则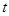 的值是
的值是  的图象上,则
的图象上,则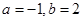



 ,则函数
,则函数 的零点为
的零点为 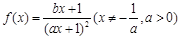 ,且
,且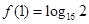 ,
,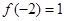
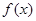 的表达式;
的表达式;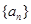 的项满足
的项满足 ,试求
,试求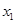 ,
,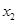 ,
,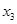 ,
,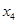 ;
;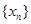 的通项;
的通项;