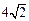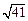题目内容
(本小题满分13分)
设 的内角
的内角 的对边分别为
的对边分别为 ,且
,且
 ,
, ,求:
,求:
(Ⅰ) 的值;
的值;
(Ⅱ) 的值.
的值.
设
 的内角
的内角 的对边分别为
的对边分别为 ,且
,且
 ,
, ,求:
,求:(Ⅰ)
 的值;
的值;(Ⅱ)
 的值.
的值.(1)
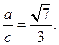
(2)

解:(Ⅰ)由余弦定理得
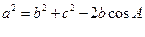
=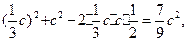
故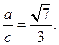 ……6分
……6分
(Ⅱ)解法一: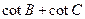
=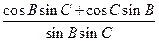
=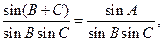 ……9分
……9分
由正弦定理和(Ⅰ)的结论得
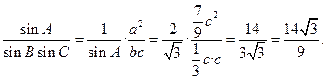
故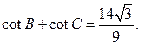 ……13分
……13分
解法二:由余弦定理及(Ⅰ)的结论有
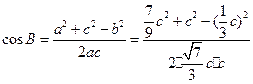
=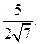
故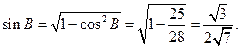
同理可得
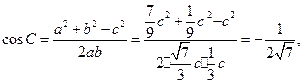
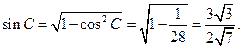
从而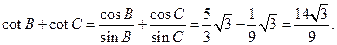
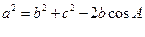
=
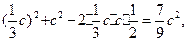
故
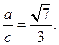 ……6分
……6分(Ⅱ)解法一:
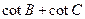
=
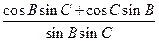
=
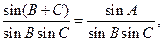 ……9分
……9分由正弦定理和(Ⅰ)的结论得
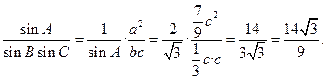
故
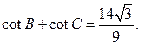 ……13分
……13分解法二:由余弦定理及(Ⅰ)的结论有
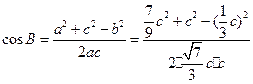
=
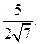
故
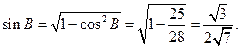
同理可得
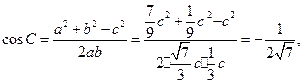
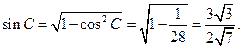
从而
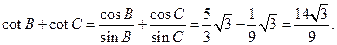

练习册系列答案
相关题目
 中,a=1,b=
中,a=1,b= , A=30°,则B等于 ( )
, A=30°,则B等于 ( ) ,AC=14,DC=6,求AD的长.
,AC=14,DC=6,求AD的长. ,
, ,则角A=( ).
,则角A=( ).



 图象的相邻两条对称轴间的距离为
图象的相邻两条对称轴间的距离为 ,且图象上一个最高点的坐标为
,且图象上一个最高点的坐标为
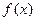 的解析式;
的解析式; 的值。
的值。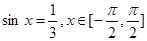 ,则
,则 =____________。(结果用反三角函数表示)
=____________。(结果用反三角函数表示)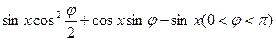 在
在 处取最小值.
处取最小值.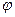 的值;
的值;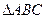 中,
中,  分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知
 ,求角C.
,求角C.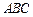 中,角
中,角
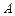 、
、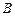 、
、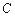 的对边分别为
的对边分别为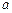 、
、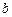 、
、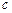 且
且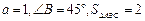 ,则
,则