题目内容
已知函数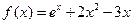 .
.
(1)求证函数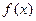 在区间
在区间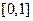 上存在唯一的极值点,并用二分法求函数取得极值时相应
上存在唯一的极值点,并用二分法求函数取得极值时相应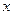 的近似值(误差不超过
的近似值(误差不超过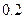 );(参考数据
);(参考数据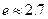 ,
,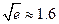 ,
,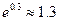 )
)
(2)当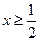 时,若关于
时,若关于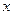 的不等式
的不等式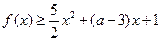 恒成立,试求实数
恒成立,试求实数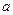 的取值范围.
的取值范围.
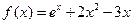 .
.(1)求证函数
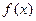 在区间
在区间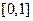 上存在唯一的极值点,并用二分法求函数取得极值时相应
上存在唯一的极值点,并用二分法求函数取得极值时相应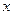 的近似值(误差不超过
的近似值(误差不超过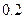 );(参考数据
);(参考数据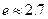 ,
,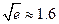 ,
,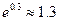 )
)(2)当
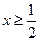 时,若关于
时,若关于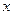 的不等式
的不等式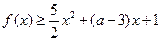 恒成立,试求实数
恒成立,试求实数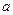 的取值范围.
的取值范围.解:(Ⅰ)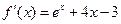 , ∵
, ∵  ,
,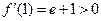 ,
,
∴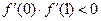 . ……………………2分
. ……………………2分
令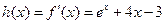 ,则
,则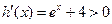 , ……………………3分
, ……………………3分
∴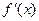 在区间
在区间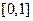 上单调递增,∴
上单调递增,∴ 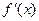 在区间
在区间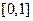 上存在唯一零点,
上存在唯一零点,
∴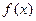 在区间
在区间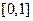 上存在唯一的极小值点. …………………………………4分
上存在唯一的极小值点. …………………………………4分
取区间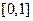 作为起始区间,用二分法逐次计算如下:
作为起始区间,用二分法逐次计算如下:
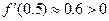 ,而
,而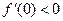 ,∴ 极值点所在区间是
,∴ 极值点所在区间是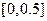 ;
;
又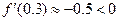 ,∴ 极值点所在区间是
,∴ 极值点所在区间是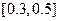 ;
;
 ③ ∵
③ ∵ 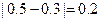 ,∴ 区间
,∴ 区间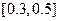 内任意一点即为所求. ……7分
内任意一点即为所求. ……7分
(Ⅱ)由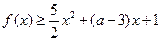 ,得
,得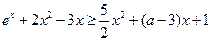 ,
,
即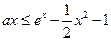 ,∵
,∵ 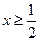 , ∴
, ∴ 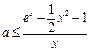 ,……………………8分
,……………………8分
令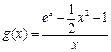 , 则
, 则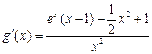 . ………………10分
. ………………10分
令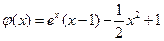 ,则
,则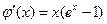 .
.
∵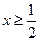 ,∴
,∴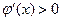 ,∴
,∴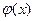 在
在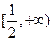 上单调递增,∴
上单调递增,∴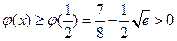 ,
,
因此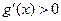 故
故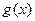 在
在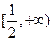 上单调递增,
上单调递增,  ……………………12分
……………………12分
则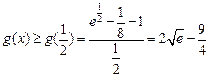 ,∴
,∴ 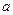 的取值范围是
的取值范围是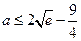 ………13分
………13分
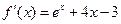 , ∵
, ∵  ,
,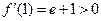 ,
,∴
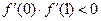 . ……………………2分
. ……………………2分令
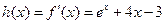 ,则
,则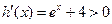 , ……………………3分
, ……………………3分∴
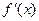 在区间
在区间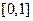 上单调递增,∴
上单调递增,∴ 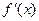 在区间
在区间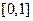 上存在唯一零点,
上存在唯一零点,∴
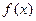 在区间
在区间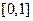 上存在唯一的极小值点. …………………………………4分
上存在唯一的极小值点. …………………………………4分取区间
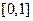 作为起始区间,用二分法逐次计算如下:
作为起始区间,用二分法逐次计算如下: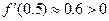 ,而
,而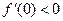 ,∴ 极值点所在区间是
,∴ 极值点所在区间是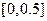 ;
;又
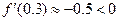 ,∴ 极值点所在区间是
,∴ 极值点所在区间是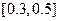 ;
; ③ ∵
③ ∵ 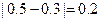 ,∴ 区间
,∴ 区间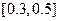 内任意一点即为所求. ……7分
内任意一点即为所求. ……7分(Ⅱ)由
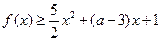 ,得
,得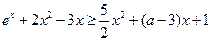 ,
,即
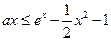 ,∵
,∵ 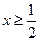 , ∴
, ∴ 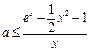 ,……………………8分
,……………………8分令
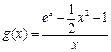 , 则
, 则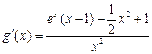 . ………………10分
. ………………10分令
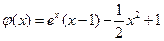 ,则
,则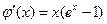 .
.∵
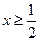 ,∴
,∴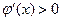 ,∴
,∴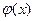 在
在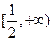 上单调递增,∴
上单调递增,∴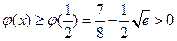 ,
,因此
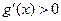 故
故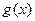 在
在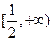 上单调递增,
上单调递增,  ……………………12分
……………………12分则
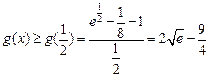 ,∴
,∴ 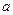 的取值范围是
的取值范围是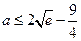 ………13分
………13分 略

练习册系列答案
相关题目
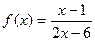 ,
,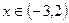
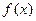 在
在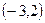 上单调递减;
上单调递减;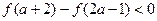 ,求
,求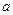 的取值范围。
的取值范围。 由下表定义:
由下表定义:
 ,
, ,
, ,则
,则 .
. 的单调递减区间是 .
的单调递减区间是 . ,用二分法求方程在(0,2)的根,则方程的根落在下面哪个区间比较精确( )
,用二分法求方程在(0,2)的根,则方程的根落在下面哪个区间比较精确( ) .(0,1) B(1,2) C.(0,
.(0,1) B(1,2) C.(0, ) D.(
) D.( 是偶函数,则在
是偶函数,则在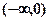 上此函数
上此函数