题目内容
在等差数列{an}中,已知a2+a3+a10+a11=36,则a5+a8=__________________________.
18
法一:根据题意,有(a1+d)+(a1+2d)+(a1+9d)+(a1+10d)=36,
∴4a1+22d=36,则2a1+11d=18.
法二:根据等差数列的性质,可得
a5+a8=a2+a11=a3+a10=36÷2=18.
∴4a1+22d=36,则2a1+11d=18.
法二:根据等差数列的性质,可得
a5+a8=a2+a11=a3+a10=36÷2=18.

练习册系列答案
相关题目
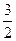 n2+
n2+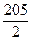 n,试求出数列{|an|}的前n项和Tn.
n,试求出数列{|an|}的前n项和Tn. ,问这个数列是等差数列吗?若是等差数列,其首项与公差分别是多少?
,问这个数列是等差数列吗?若是等差数列,其首项与公差分别是多少?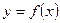 的图像经过坐标原点,且
的图像经过坐标原点,且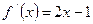 ,数列
,数列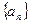 的前
的前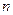 项和
项和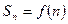
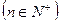
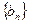 满足
满足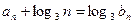 ,求数列
,求数列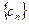 满足
满足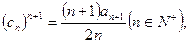 求数列
求数列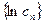 中的最大值。
中的最大值。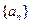 满足
满足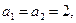
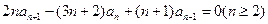 ,
,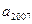 的值
的值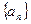 的各项均为正数,若
的各项均为正数,若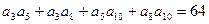 ,
,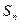 为
为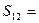 ______________。
______________。