题目内容
(本题满分12分)
设函数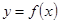 满足:对任意的实数
满足:对任意的实数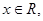 有
有
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若方程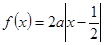 有解,求实数
有解,求实数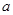 的取值范围.
的取值范围.
设函数
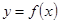 满足:对任意的实数
满足:对任意的实数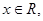 有
有
(Ⅰ)求
 的解析式;
的解析式;(Ⅱ)若方程
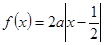 有解,求实数
有解,求实数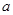 的取值范围.
的取值范围.(1)  (2)
(2) 
 (2)
(2) 
试题分析:解:⑴
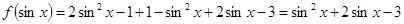
所以
 …………………5分
…………………5分⑵①当
 时,
时, 不成立.
不成立.②当
 时,
时, 令
令 则
则


因为函数
 在
在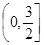 上单增,所以
上单增,所以
③当
 时,
时, 令
令 则
则


因为函数
 在
在 上单增,所以
上单增,所以
综上,实数
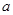 的取值范围是
的取值范围是 ……………………12分
……………………12分点评:解决该试题的关键是理解换元法的思想,整体代换得到解析式,同时能将方程有解问题,通过分离变量的方法来运用图像与图像的交点问题来得到。而参数的取值范围即为函数的值域,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
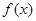 是定义在
是定义在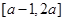 上的偶函数,且当
上的偶函数,且当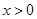 时,
时,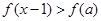 的解集为 ( )
的解集为 ( )

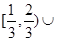
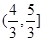
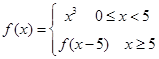 ,那么
,那么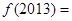 ( )
( )

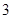
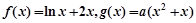 .
. ,求
,求 的单调区间;
的单调区间; 恒成立,求
恒成立,求 的取值范围.
的取值范围. 分)
分) 在定义域
在定义域 内某区间
内某区间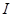 上是增函数,而
上是增函数,而 在
在 在
在 ,
, 在
在 是否是“弱增函数”,
是否是“弱增函数”, (
( 是常数且
是常数且 )在
)在 上是“弱增函数”.
上是“弱增函数”. 的单调增区间是_________
的单调增区间是_________ 上是增函数的是 ( )
上是增函数的是 ( )



 是以
是以 为周期的偶函数,当
为周期的偶函数,当 时,
时, .若关于
.若关于 的方程
的方程 (
( )在区间
)在区间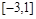 内有四个不同的实根,则
内有四个不同的实根,则 的取值范围是
的取值范围是


