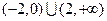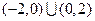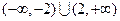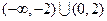题目内容
(本小题满分14分)
 设函数
设函数 ,函数
,函数 有唯一的零点,其中实数
有唯一的零点,其中实数 为常数,
为常数, ,
, .
.
(Ⅰ)求 的表达式;(Ⅱ)求
的表达式;(Ⅱ)求 的值;
的值;
(Ⅲ)若 且
且 ,求证:
,求证: .
.
 设函数
设函数 ,函数
,函数 有唯一的零点,其中实数
有唯一的零点,其中实数 为常数,
为常数, ,
, .
.(Ⅰ)求
 的表达式;(Ⅱ)求
的表达式;(Ⅱ)求 的值;
的值;(Ⅲ)若
 且
且 ,求证:
,求证: .
.解:(1)由于
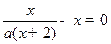 ,
,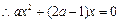 -------2分
-------2分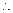 当且仅当
当且仅当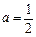 时,函数
时,函数 有唯一零点.
有唯一零点. 从而
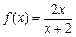
 -------4分
-------4分(2)由已知
 ,得
,得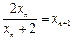 -------5分
-------5分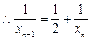 ,即
,即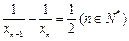
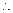 数列
数列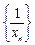 是以
是以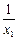 为首项,
为首项,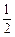 为公差的等差数列. -------6分
为公差的等差数列. -------6分 ,
,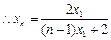
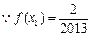 ,
,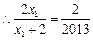 ,即
,即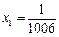
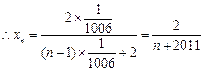 -------7分
-------7分故
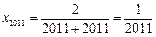 -------8分
-------8分(3)证明
 :
: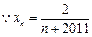 ,
,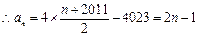 -------10分
-------10分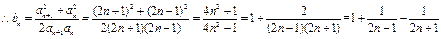 ---
--- 12分
12分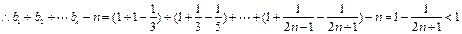 --13分
--13分故
 -------14分
-------14分略

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
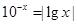 的两根为
的两根为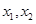 ,则 ( )
,则 ( )



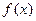 对任意的
对任意的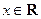 ,均有
,均有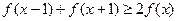 ,则称函数
,则称函数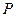 .
.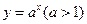 ; ②
; ②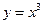 .
.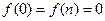 (
(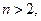
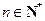 ),
),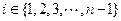 有
有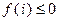 ;
;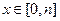 均有
均有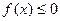 .若成立给出证明,若不成立给出反例.
.若成立给出证明,若不成立给出反例. 的大致图象,则
的大致图象,则 等于( )
等于( ) B
B  C
C  D
D 

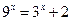 的解为 ▲ .
的解为 ▲ .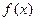 的定义域为
的定义域为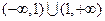 ,且
,且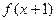 为奇函数,当
为奇函数,当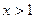 时,
时, 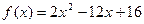 ,则直线
,则直线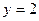 与函数
与函数
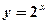 与
与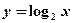 的图像关于直线
的图像关于直线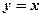 对称;②为了得到函数
对称;②为了得到函数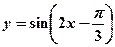 的图象,只需把函数
的图象,只需把函数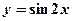 的图象上的所有点向右平移
的图象上的所有点向右平移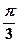 个单位长度; ③当
个单位长度; ③当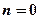 或
或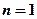 时,
时, 幂函数
幂函数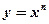 的图象都是一条直线;④已知函数
的图象都是一条直线;④已知函数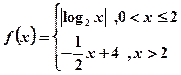 ,
, 若
若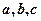 互不相等,且
互不相等,且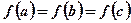 ,则
,则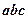 的取值
的取值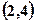 .
. 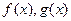 分别是定义在
分别是定义在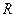 上的奇函数和偶函数,当
上的奇函数和偶函数,当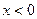 时,
时,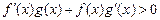 且
且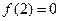
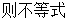
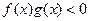 的解集为
的解集为