题目内容
已知 是直线,
是直线,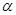 是平面,
是平面,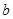 、
、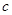
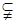
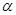 ,则“
,则“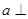 平面
平面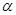 ”是“
”是“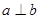 且
且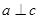 ”的 ………………………………………………………………………… ( )
”的 ………………………………………………………………………… ( )
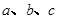 是直线,
是直线,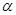 是平面,
是平面,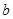 、
、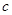
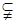
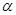 ,则“
,则“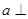 平面
平面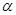 ”是“
”是“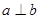 且
且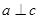 ”的 ………………………………………………………………………… ( )
”的 ………………………………………………………………………… ( )| A.充要条件. | B.充分非必要条件. | C.必要非充分条件. | D.非充分非必要条件 |
B
由垂直的定义,我们易得“a⊥b且a⊥c”?“a⊥平面α”为假命题,反之“a⊥平面α”?“a⊥b且a⊥c”为真命题,根据充要条件的定义,即可得到结论.
解答:解:直线与平面α内的无数条平行直线垂直,但该直线未必与平面α垂直;
即“a⊥b且a⊥c”?“a⊥平面α”为假命题;
但直线l与平面α垂直时,l与平面α内的每一条直线都垂直,
即“a⊥平面α”?“a⊥b且a⊥c”为真命题;
“a⊥平面α”是“a⊥b且a⊥c”的充分非必要条件
故选B
点评:判断充要条件的方法是:①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.
解答:解:直线与平面α内的无数条平行直线垂直,但该直线未必与平面α垂直;
即“a⊥b且a⊥c”?“a⊥平面α”为假命题;
但直线l与平面α垂直时,l与平面α内的每一条直线都垂直,
即“a⊥平面α”?“a⊥b且a⊥c”为真命题;
“a⊥平面α”是“a⊥b且a⊥c”的充分非必要条件
故选B
点评:判断充要条件的方法是:①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
相关题目

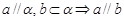

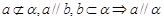
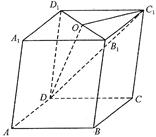
 α,b
α,b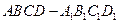 中,若
中,若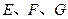 分别为棱
分别为棱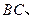
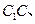
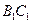 的中点,
的中点,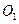 、
、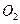 分别为四边形
分别为四边形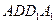 、
、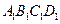 的中心,则下列各组中的四个点不在同一个平面上的是( )
的中心,则下列各组中的四个点不在同一个平面上的是( )