题目内容
请先阅读:
设可导函数 f(x) 满足f(-x)=-f(x)(x∈R).
在等式f(-x)=-f(x) 的两边对x求导,
得(f(-x))′=(-f(x))′,
由求导法则,得f′(-x)•(-1)=-f′(x),
化简得等式f′(-x)=f′(x).
(Ⅰ)利用上述想法(或其他方法),结合等式(1+x)n=
+
x+
x2+…+
xn(x∈R,整数n≥2),证明:n[(1+x)n-1-1]=2
x+3
x2+4
x3+…+n
xn-1;
(Ⅱ)当整数n≥3时,求
-2
+3
-…+(-1)n-1n
的值;
(Ⅲ)当整数n≥3时,证明:2
-3•2
+4•3
+…+(-1)n-2n(n-1)
=0.
设可导函数 f(x) 满足f(-x)=-f(x)(x∈R).
在等式f(-x)=-f(x) 的两边对x求导,
得(f(-x))′=(-f(x))′,
由求导法则,得f′(-x)•(-1)=-f′(x),
化简得等式f′(-x)=f′(x).
(Ⅰ)利用上述想法(或其他方法),结合等式(1+x)n=
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
(Ⅱ)当整数n≥3时,求
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
(Ⅲ)当整数n≥3时,证明:2
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
分析:(I)在等式(1+x)n=Cn0+Cn1x+Cn2x2++Cnnxn,两边对x求导,整理可得结论;
(II)当整数n≥3时,n(1+x)n-1=Cn1+2Cn2x+…+(n-1)Cnn-1xn-2+nCnnxn-1中,令x=-1,可得结论;
(III)当整数n≥3时,n(1+x)n-1=Cn1+2Cn2x+…+(n-1)Cnn-1xn-2+nCnnxn-1中,两边对x求导,令x=-1,可得结论.
(II)当整数n≥3时,n(1+x)n-1=Cn1+2Cn2x+…+(n-1)Cnn-1xn-2+nCnnxn-1中,令x=-1,可得结论;
(III)当整数n≥3时,n(1+x)n-1=Cn1+2Cn2x+…+(n-1)Cnn-1xn-2+nCnnxn-1中,两边对x求导,令x=-1,可得结论.
解答:(Ⅰ)证明:在等式(1+x)n=Cn0+Cn1x+Cn2x2++Cnnxn
两边对x求导得n(1+x)n-1=Cn1+2Cn2x+…+(n-1)Cnn-1xn-2+nCnnxn-1
移项得n[(1+x)n-1-1]=2
x+3
x2+4
x3+…+n
xn-1;
(Ⅱ)解:当整数n≥3时,n(1+x)n-1=Cn1+2Cn2x+…+(n-1)Cnn-1xn-2+nCnnxn-1中,令x=-1,可得
-2
+3
-…+(-1)n-1n
=(-1)n-1n;
(Ⅲ)证明:当整数n≥3时,∵n(1+x)n-1=Cn1+2Cn2x+…+(n-1)Cnn-1xn-2+nCnnxn-1,
求导函数,可得(n-1)n(1+x)n-2=+2Cn2+…+n(n-1)Cnnxn-2,
令x=-1,可得2
-3•2
+4•3
+…+(-1)n-2n(n-1)
=0.
两边对x求导得n(1+x)n-1=Cn1+2Cn2x+…+(n-1)Cnn-1xn-2+nCnnxn-1
移项得n[(1+x)n-1-1]=2
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
(Ⅱ)解:当整数n≥3时,n(1+x)n-1=Cn1+2Cn2x+…+(n-1)Cnn-1xn-2+nCnnxn-1中,令x=-1,可得
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
(Ⅲ)证明:当整数n≥3时,∵n(1+x)n-1=Cn1+2Cn2x+…+(n-1)Cnn-1xn-2+nCnnxn-1,
求导函数,可得(n-1)n(1+x)n-2=+2Cn2+…+n(n-1)Cnnxn-2,
令x=-1,可得2
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
点评:本题考查二项式定理的运用,考查导数知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
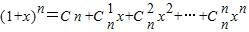 (x∈R,整数n≥2),证明:
(x∈R,整数n≥2),证明: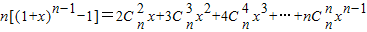 ;
; 的值;
的值;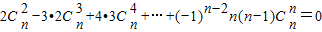 .
.