题目内容
CD是直角三角形ABC斜边上的高，BD=2AD，将△ACD绕CD旋转到△A′CD，使二面角A′-CD-B为60°．
（1）求证：BA′⊥面A′CD；
（2）求异面直线A′C与BD所成角的余弦．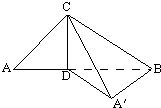
（1）求证：BA′⊥面A′CD；
（2）求异面直线A′C与BD所成角的余弦．
证明：（1）∵BD=2AD
∴BD=2AD
∵二面角A′-CD-B为60°，∠BDA为二面角A′-CD-B的平面角
∴∠BDA=60°
∴△BAA′D为直角三角形
∴A′D⊥A′B
又∵CD⊥A′B，CD∩A′D=D
∴BA′⊥面A′CD
（2）过A′作BD的平行线A′E然后构造平行四边形BA′DE
∴根据异面直线所成的角的定义可得∠CA′E异面直线A′C与BD所成角
设AD=1
∴BD=2，A′B=
，CD=
，A′D=1，CE=
∴由余弦定理得：cos∠CA′E=
=
即异面直线A′C与BD所成角的余弦为
∴BD=2AD
∵二面角A′-CD-B为60°，∠BDA为二面角A′-CD-B的平面角
∴∠BDA=60°
∴△BAA′D为直角三角形
∴A′D⊥A′B
又∵CD⊥A′B，CD∩A′D=D
∴BA′⊥面A′CD
（2）过A′作BD的平行线A′E然后构造平行四边形BA′DE
∴根据异面直线所成的角的定义可得∠CA′E异面直线A′C与BD所成角
设AD=1
∴BD=2，A′B=
| 3 |
| 2 |
| 5 |
∴由余弦定理得：cos∠CA′E=
| A′C2+A′E2- EC2 |
| 2A′C•A′E |
| ||
| 6 |
即异面直线A′C与BD所成角的余弦为
| ||
| 6 |
练习册系列答案
相关题目
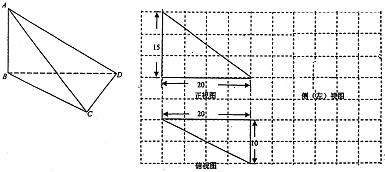如图，在三棱锥A-BCD中，AB⊥平面BCD，它的正视图和俯视图都是直角三角形，图中尺寸单位为cm．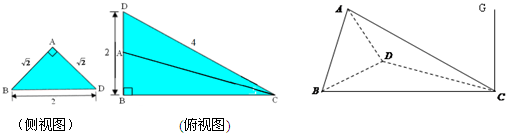
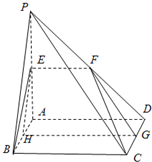如图，平面PAD⊥平面ABCD，四边形ABCD为正方形，△PAD是直角三角形，且PA=AD=2，E，F，G，H分别是线段PA，PD，CD，AB的中点．
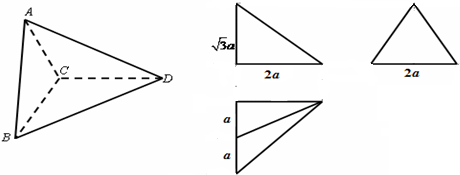某几何体的直观图与三视图如下，其中主视图、俯视图都是直角三角形，左视图是等边三角形．