题目内容
9.已知直线l过点M(1,1),且与x轴,y轴的正半轴分别相交于A,B两点,O为坐标原点.求:(1)当|OA|十|OB|取得最小值时,直线l的方程;
(2)当|MA|2+|MB|2取得最小值时,直线l的方程.
分析 (1)设出点A的坐标,写出直线AB的方程,利用基本不等式求出a+b=|OA|+|OB|的最小值,写出对应的直线方程;
(2)设出直线方程为y-1=k(x-1)(k<0),求出|MA|2+|MB|2的最小值,写出对应的直线方程.
解答 解:(1)设点A(a,0),B(0,b),且a>0,b>0,
直线l的方程为:$\frac{x}{a}$+$\frac{y}{b}$=1,
且直线l过点M(1,1),∴$\frac{1}{a}$+$\frac{1}{b}$=1①;
∴a+b=(a+b)•($\frac{1}{a}$+$\frac{1}{b}$)=2+$\frac{a}{b}$+$\frac{b}{a}$≥2+2$\sqrt{\frac{a}{b}•\frac{b}{a}}$=4,
当且仅当$\frac{a}{b}$=$\frac{b}{a}$,即a=b时取“=”,
将a=b代入①式得a=2,b=2;
∴直线l的方程为x+y-2=0,
即|OA|+|OB|取最小值4时,l的方程为x+y-2=0;
(2)设直线方程为y-1=k(x-1)(k<0),
则A(-$\frac{1}{k}$+1,0),B(0,1-k),
∴|MA|2+|MB|2=[(-$\frac{1}{k}$)2+1]+[1+(-k)2]=2+k2+$\frac{1}{{k}^{2}}$≥2+2•k2•$\frac{1}{{k}^{2}}$=4,
当且仅当k=-1时取“=”;
∴当|MA|2+|MB|2取得最小值4时,直线l的方程为y-1=-(x-1),即x+y-2=0.
点评 本题考查了两点间的距离公式及基本不等式和直线方法的应用问题,是综合性题目.

练习册系列答案
相关题目
17.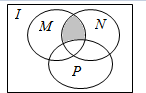 设I是全集,集合M,N,P都是其子集,则图中的阴影部分表示的集合为( )
设I是全集,集合M,N,P都是其子集,则图中的阴影部分表示的集合为( )
 设I是全集,集合M,N,P都是其子集,则图中的阴影部分表示的集合为( )
设I是全集,集合M,N,P都是其子集,则图中的阴影部分表示的集合为( )| A. | M∩(P∩∁IN) | B. | M∩(N∩∁IP) | C. | M∩(∁IN∩∁IM) | D. | (M∩N)∪(M∩P) |
18.已知点A,B,C,D为同一球面上的四点,且AB=AC=AD=2,AB⊥AC,AC⊥AD,AD⊥AB,则这个球的表面积是( )
| A. | 16π | B. | 20π | C. | 12π | D. | 8π |
19.设f(x)=|2x-1|,若关于x的函数g(x)=(1-t)f2(x)-f(x)+t有三个零点,则实数t的取值范围为( )
| A. | (0,$\frac{1}{2}$) | B. | (-∞,$\frac{1}{2}$)∪(1,+∞) | C. | ($\frac{1}{2},1$) | D. | [0,1) |
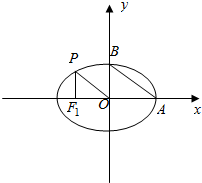 已知A、B分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右顶点、上顶点,过左焦点F1作PF1⊥x轴,与椭圆在x轴上方的交点为P,且OP∥AB.
已知A、B分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右顶点、上顶点,过左焦点F1作PF1⊥x轴,与椭圆在x轴上方的交点为P,且OP∥AB.