题目内容
1.已知:sinx+siny=$\frac{1}{3}$,求cosx+cosy的取值范围.分析 设cosx+cosy=a,两式平方后相加,求出a2的范围,利用余弦函数的值域即可确定出a的范围.
解答 解:设cosx+cosy=a①,
由sinx+siny=$\frac{1}{3}$②,①2+②2得:(sinx+siny)2+(cosx+cosy)2=$\frac{1}{9}$+a2,
整理得:2+2(cosxcosy+sinxsiny)=$\frac{1}{9}$+a2,即2+2cos(x-y)=$\frac{1}{9}$+a2,
解得:a2=$\frac{17}{9}$+2cos(x-y),
∵-1≤cos(x-y)≤1,即0≤a2≤$\frac{35}{9}$,
∴0≤a≤$\frac{\sqrt{35}}{3}$或-$\frac{\sqrt{35}}{3}$≤a<0,
则cosx+cosy的范围为[-$\frac{\sqrt{35}}{3}$,0)∪[0,$\frac{\sqrt{35}}{3}$].
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
11.如图所示的程序框图中,若x=5,则输出i的值是( )
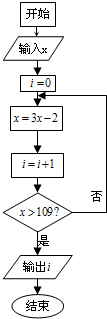

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
12.执行如图的程序框图,若输入m的值为2,则输出的结果i=( )
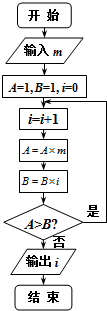

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
6.设正实数x,y,z满足x2-7xy+16y2-z=0,则当$\frac{z}{xy}$取得最小值时,x+2y-z的最大值为( )
| A. | 0 | B. | $\frac{9}{8}$ | C. | $\frac{9}{4}$ | D. | 2 |
13.散点图在回归分析过程中的作用是( )
| A. | 查找个体个数 | B. | 粗略判断变量是否线性相关 | ||
| C. | 探究个体分类 | D. | 比较个体数据大小关系 |
10.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),两个焦点分别为F1、F2,若在第一象限内双曲线上存在一点P,使得在△PF1F2中,∠PF1F2=30°,∠PF2F1=90°,则此双曲线的渐近线方程为( )
| A. | $y=±\frac{{\sqrt{2}}}{2}x$ | B. | $y=±\sqrt{2}x$ | C. | $y=±\sqrt{3}x$ | D. | y=±2x |
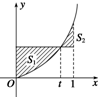 在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为($\frac{1}{2}$,1).
在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为($\frac{1}{2}$,1).