题目内容
【题目】已知函数f（x）=|x﹣a|﹣|x﹣2|．
（1）当a=﹣3时，求不等式f（x）＜2的解集；
（2）若x∈[1，2]时不等式f（x）＜2成立，求实数a的取值范围．
【答案】（1）不等式的解集为{x|x＜
}；（2）实数a的取值范围是﹣2＜a＜4.
【解析】
（1）a=﹣3时，f（x）=|x+3|﹣|x﹣2|，零点分区间，去掉绝对值，分段解不等式即可；（2）原式等价于|x﹣a|＜2+|x﹣2|成立，即2x﹣4＜a＜4，而y=2x﹣4在[1，2]上的最小值为﹣2,进而得到参数范围.
（1）函数f（x）=|x﹣a|﹣|x﹣2|，
当a=﹣3时，f（x）=|x+3|﹣|x﹣2|=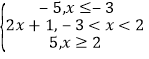
；
则x≤﹣3时，不等式f（x）＜2化为﹣5＜2，∴x≤﹣3；
﹣3＜x＜2时，不等式f（x）＜2化为2x+1＜2，∴﹣3＜x＜；
x≥2时，不等式f（x）＜2化为5＜2，∴x∈；
综上，不等式的解集为{x|x＜}；
（2）x∈[1，2]时不等式f（x）＜2成立，
即|x﹣a|﹣|x﹣2|＜2成立，
等价于|x﹣a|＜2+|x﹣2|成立；
∴|x﹣a|＜4﹣x，
∴x﹣4＜x﹣a＜4﹣x，
即2x﹣4＜a＜4；
又y=2x﹣4在[1，2]上的最小值为﹣2，
∴实数a的取值范围是﹣2＜a＜4．
【题目】某单位计划在一水库建一座至多安装3台发电机的水电站，过去50年的水文资料显示，水库年入流量
（年入流量：一年内上游来水与库区降水之和，单位：亿立方米）都在40以上，不足80的年份有10年，不低于80且不超过120的年份有35年，超过120的年份有5年，将年入流量在以上三段的频率作为相应段的概率，假设各年的年入流量相互独立.
（1）求未来3年中，设
表示流量超过120的年数，求的分布列及期望；
（2）水电站希望安装的发电机尽可能运行，但每年发电机最多可运行台数受年入流量限制，并有如下关系：
年入流量 |
|
|
|
发电机最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行，则该台年利润为5000万元，若某台发电机未运行，则该台年亏损800万元，欲使水电站年总利润的均值达到最大，应安装发电机多少台？
【题目】近年来，国资委.党委高度重视扶贫开发工作，坚决贯彻落实中央扶贫工作重大决策部署，在各个贫困县全力推进定点扶贫各项工作，取得了积极成效，某贫困县为了响应国家精准扶贫的号召，特地承包了一块土地，已知土地的使用面积以及相应的管理时间的关系如下表所示：
土地使用面积 |
|
|
|
|
|
管理时间 |
|
|
|
|
|
并调查了某村
名村民参与管理的意愿，得到的部分数据如下表所示：
愿意参与管理 | 不愿意参与管理 | |
男性村民 |
|
|
女性村民 |
|
求出相关系数
的大小，并判断管理时间
与土地使用面积
是否线性相关？
若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况，则从该贫困县中任取
人，记取到不愿意参与管理的男性村民的人数为
，求的分布列及数学期望.
参考公式：
，参考数据：
，
，
