题目内容
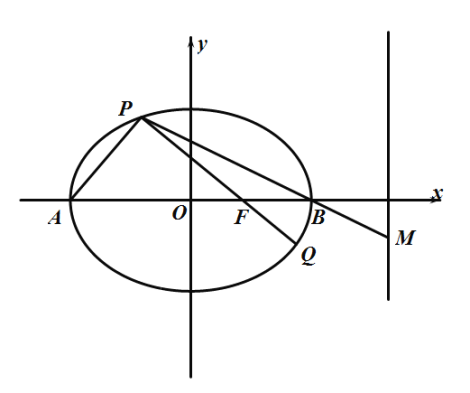
【题目】如图,A,B为椭圆![]() 的左、右顶点,直线
的左、右顶点,直线![]() 过椭圆C的右焦点F且交椭圆于P,Q两点.连结
过椭圆C的右焦点F且交椭圆于P,Q两点.连结![]() 并延长交直线
并延长交直线![]() 于点M.
于点M.
(1)若直线![]() 的斜率为
的斜率为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)求证:A,Q,M三点共线.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)设![]() ,计算出
,计算出![]() 的值,最后求出直线
的值,最后求出直线![]() 的斜率,最后求出直线
的斜率,最后求出直线![]() 的方程;
的方程;
(2)根据直线![]() 的斜率为零不为零进行分类讨论. 直线
的斜率为零不为零进行分类讨论. 直线![]() 的斜率为零时,显然成立;直线
的斜率为零时,显然成立;直线![]() 的斜率不为零时,设出直线的方程与椭圆方程联立,利用根与系数的关系,只要计算出
的斜率不为零时,设出直线的方程与椭圆方程联立,利用根与系数的关系,只要计算出![]() 就可以证明出A,Q,M三点共线.
就可以证明出A,Q,M三点共线.
(1)设![]() ,所以
,所以![]() ,由题意可知:
,由题意可知:![]() ,
,
则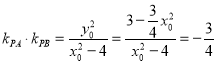 .
.
∴![]() ,∴直线
,∴直线![]() 的方程为:
的方程为:![]()
(2)当![]() 垂直于y轴时,方程为
垂直于y轴时,方程为![]() ,此时显然有A,Q,M三点共线;
,此时显然有A,Q,M三点共线;
当![]() 不垂直于y轴时,设
不垂直于y轴时,设![]() 方程为
方程为![]() ,
,![]() ,
,![]()
则直线![]() 方程为
方程为![]() ,令
,令![]() 得,
得,![]() ,即
,即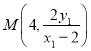 .
.
![]()
∴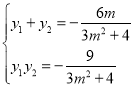
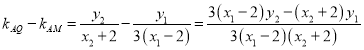
∵![]()
![]()
∴![]()
∴A,Q,M三点共线.

练习册系列答案
相关题目