题目内容
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 上的动点.
上的动点.
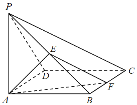
(1)求证:平面![]() 平面
平面![]() .
.
(2)试确定点![]() 的位置,使平面
的位置,使平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() .
.
【答案】(1)见解析; (2)点F为BC中点.
【解析】
(1)利用直线与平面垂直的性质、判定定理以及平面与平面垂直的判定定理证明即可.(2)找建立空间直角坐标系,分别求出平面![]() 与平面
与平面![]() 的法向量,利用数量积求出法向量间夹角,进而得到二面角的余弦值。
的法向量,利用数量积求出法向量间夹角,进而得到二面角的余弦值。
(1)因为![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() .
.
因为![]() 为正方形,所以
为正方形,所以![]() ,
,
又因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() .
.
因为![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,
所以![]() ,
,
又因为![]() ,
,
所以![]() 平面
平面![]()
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)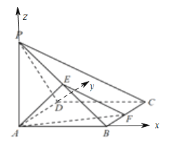
因为![]() 底面
底面![]() ,
,![]() ,以
,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向,建立如图所示的空间直角坐标系
轴的正方向,建立如图所示的空间直角坐标系![]() ,
,
设正方形![]() 的边长为2,则
的边长为2,则![]() ,
,
所以![]()
设点![]() 的坐标为
的坐标为![]() 所以
所以![]()
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则 所以
所以
取![]() ,则
,则![]() .
.
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则 所以
所以
取![]() ,则
,则![]() .
.
因为平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,
,
所以![]() ,
,
解得![]() ,
,
故当点![]() 为
为![]() 中点时,平面
中点时,平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() .
.

【题目】目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如下图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.

(1)求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长潜伏者”的人数;
(2)为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取300人,得到如下列联表,请将列联表补充完整,并根据列联表判断是否有97.5%的把握认为潜伏期长短与患者年龄有关;
短潜伏者 | 长潜伏者 | 合计 | |
60岁及以上 | 90 | ||
60岁以下 | 140 | ||
合计 | 300 |
(3)研究发现,某药物对新冠病毒有一定的抑制作用,需要在抽取的300人中分层选取7位60岁以下的患者做Ⅰ期临床试验,再从选取的7人中随机抽取两人做Ⅱ期临床试验,求两人中恰有1人为“长潜伏者”的概率.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

【题目】工厂质检员从生产线上每半个小时抽取一件产品并对其某个质量指标![]() 进行检测,一共抽取了
进行检测,一共抽取了![]() 件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标
件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标![]() 有关,具体见下表.
有关,具体见下表.
质量指标 |
|
|
|
频数 |
|
|
|
一年内所需维护次数 |
|
|
|
(1)以每个区间的中点值作为每组指标的代表,用上述样本数据估计该厂产品的质量指标![]() 的平均值(保留两位小数);
的平均值(保留两位小数);
(2)用分层抽样的方法从上述样本中先抽取![]() 件产品,再从
件产品,再从![]() 件产品中随机抽取
件产品中随机抽取![]() 件产品,求这
件产品,求这![]() 件产品的指标
件产品的指标![]() 都在
都在内的概率;
(3)已知该厂产品的维护费用为![]() 元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加
元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加![]() 元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这
元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这![]() 件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?