题目内容
设函数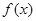 的定义域为
的定义域为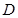 ,如果
,如果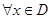 ,存在唯一的
,存在唯一的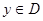 ,使
,使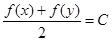 (
(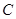 为常数)成立。则称函数
为常数)成立。则称函数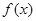 在
在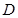 上的“均值”为
上的“均值”为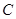 。已知四个函数:
。已知四个函数:
①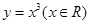 ;②
;②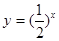
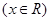 ;③
;③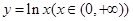 ;④
;④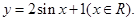
上述四个函数中,满足所在定义域上“均值”为1的函数是 .(填入所有满足条件函数的序号)
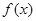 的定义域为
的定义域为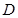 ,如果
,如果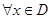 ,存在唯一的
,存在唯一的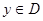 ,使
,使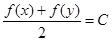 (
(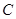 为常数)成立。则称函数
为常数)成立。则称函数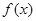 在
在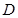 上的“均值”为
上的“均值”为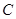 。已知四个函数:
。已知四个函数:①
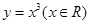 ;②
;②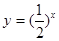
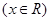 ;③
;③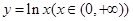 ;④
;④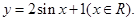
上述四个函数中,满足所在定义域上“均值”为1的函数是 .(填入所有满足条件函数的序号)
①③④
试题分析:根据在其定义域上均值为1的函数的定义,逐一对四个函数列出方程,解出y关于x的表达式,其中①③④在其定义域内有解,②在其定义域内无解,从而得出正确答案.
解:①对于函数
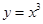 ,定义域为
,定义域为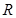 ,设
,设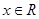 ,由
,由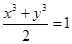 ,得
,得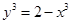 ,所以
,所以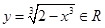
,所以函数
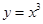 是定义域上的“均值”为1的函数;
是定义域上的“均值”为1的函数;②对于函数
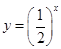 ,定义域为
,定义域为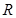 ,设
,设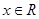 ,由
,由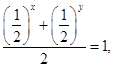 得:
得: 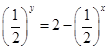 ,
,当
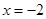 时 ,
时 ,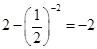 ,不存在实数
,不存在实数 的值,使
的值,使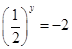 ,所以该函数不是定义域上均值为1的函数;
,所以该函数不是定义域上均值为1的函数;③对于函数
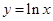 ,定义域是
,定义域是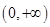 ,设
,设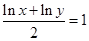 ,得
,得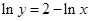 ,则
,则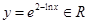 ,
,所以该函数是定义域上的均值为1的函数;
④对于函数
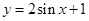 ,定义域为
,定义域为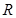 ,设
,设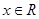 ,由
,由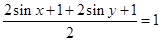 ,得
,得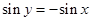 ,因为
,因为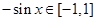 所以存在实数
所以存在实数 ,使得
,使得 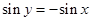 成立,所以函数
成立,所以函数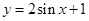 在其定义域上是均值为1的函数.
在其定义域上是均值为1的函数.
练习册系列答案
相关题目
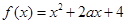 ,
,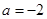 ,求方程
,求方程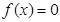 的根;
的根;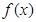 满足
满足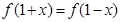 ,求函数在
,求函数在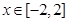 的值域.
的值域.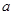 是实数,
是实数,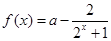
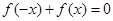 成立;
成立;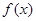 均为增函数
均为增函数 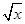 在[0,+∞)上是增函数,则a=________.
在[0,+∞)上是增函数,则a=________.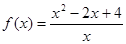 (
(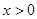 )的值域是___________.
)的值域是___________.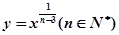 的定义域为
的定义域为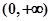 ,且单调递减,则
,且单调递减,则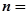 __________.
__________.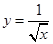 的定义域为 .
的定义域为 .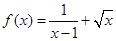 的定义域为( )
的定义域为( )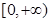

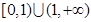
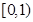
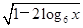 的定义域为______.
的定义域为______.