题目内容
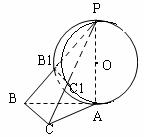
(12分)如图,在三棱锥P—ABC中,PA⊥底面ABC,∠BAC=60°,AB=AC=2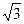 ,以PA为直径的球O和PB、PC分别交于B1、C1
,以PA为直径的球O和PB、PC分别交于B1、C1
(1)求证B1C1∥平面ABC
(2)若二面角C—PB—A的大小为arctan2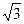 ,试求球O的表面积。
,试求球O的表面积。
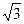 ,以PA为直径的球O和PB、PC分别交于B1、C1
,以PA为直径的球O和PB、PC分别交于B1、C1(1)求证B1C1∥平面ABC
(2)若二面角C—PB—A的大小为arctan2
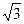 ,试求球O的表面积。
,试求球O的表面积。
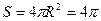
(12分)
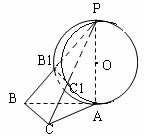
(1)连接AC1、AB1
∵PA⊥底面ABC
∴PA⊥AB、PA⊥AC
又∵AB=AC,易得△APC≌△APB
∴BP=CP
∠APB1=∠APC1
∵AP为球O的直径,∴AC1⊥PC1
AB1⊥PB1 ∴cos∠APB1=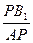 =cos∠APC1=
=cos∠APC1=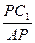
∴PB1=PC1……………………(3分)
∴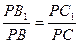 ∴B1C1∥BC
∴B1C1∥BC
又∵B1C1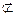 平面ABC,BC
平面ABC,BC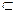 平面ABC
平面ABC
∴B1C1∥平面ABC …………………………(6分)
(2)过点C作CD⊥AB于点D,则CD⊥平面ABP,过D作DE⊥PB于E,连CE,由三垂线定理知CE⊥PB
∴∠CED是二面角C—PB—A的平面角,即∠CED=arctan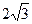
∴tan∠CED=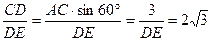
∴DE=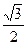
sin∠PBA=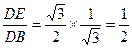
∴∠PBA=30°…………(9分)
∴AP=ABtan∠PBA=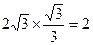
∴球O的半径R=1………………(11分)
∴球O的表面积为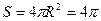 …………(12分)
…………(12分)

(1)连接AC1、AB1
∵PA⊥底面ABC
∴PA⊥AB、PA⊥AC
又∵AB=AC,易得△APC≌△APB
∴BP=CP
∠APB1=∠APC1
∵AP为球O的直径,∴AC1⊥PC1
AB1⊥PB1 ∴cos∠APB1=
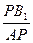 =cos∠APC1=
=cos∠APC1=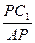
∴PB1=PC1……………………(3分)
∴
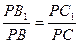 ∴B1C1∥BC
∴B1C1∥BC又∵B1C1
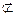 平面ABC,BC
平面ABC,BC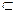 平面ABC
平面ABC∴B1C1∥平面ABC …………………………(6分)
(2)过点C作CD⊥AB于点D,则CD⊥平面ABP,过D作DE⊥PB于E,连CE,由三垂线定理知CE⊥PB
∴∠CED是二面角C—PB—A的平面角,即∠CED=arctan
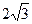
∴tan∠CED=
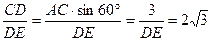
∴DE=
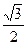
sin∠PBA=
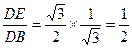
∴∠PBA=30°…………(9分)
∴AP=ABtan∠PBA=
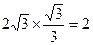
∴球O的半径R=1………………(11分)
∴球O的表面积为
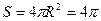 …………(12分)
…………(12分)
练习册系列答案
相关题目
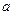 的正方体
的正方体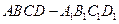 中,
中,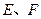 分别是
分别是 的中点,
的中点,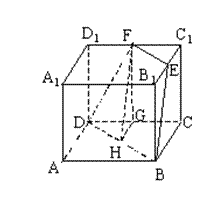
 四点共面;
四点共面; 的面积.
的面积.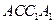 成45°角,AB=4cm,求这个棱柱的侧面积。(12分)
成45°角,AB=4cm,求这个棱柱的侧面积。(12分)
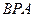 =
=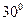 ,
,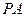 =
=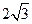 ,
,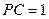 ,求圆
,求圆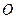 的半径。
的半径。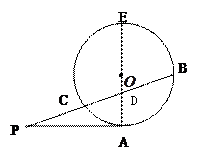
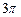 ,则该四面体的棱长为 (※)
,则该四面体的棱长为 (※)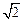
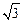
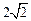
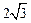
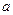 的正方体
的正方体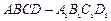 中,P、Q是对角
中,P、Q是对角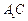 上的点,若
上的点,若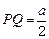 ,则三棱锥
,则三棱锥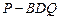 的体积为 ________
的体积为 ________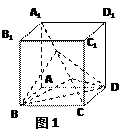
 为球心的球面上,则球
为球心的球面上,则球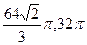 B.
B. 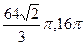 C.
C. 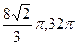 D.
D.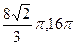
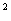 ,则此球的体积为____
,则此球的体积为____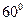 ,则该正四棱锥的侧面积是 .
,则该正四棱锥的侧面积是 .