题目内容
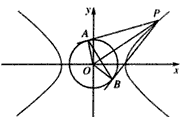
已知双曲线C: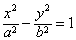 (a>b>0)和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x0,y0)引圆O的两条切线,切点分别为A,B。
(a>b>0)和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x0,y0)引圆O的两条切线,切点分别为A,B。
(1)若双曲线C上存在点P,使得∠APB=90°,求双曲线离心率e的取值范围;
(2)求直线AB的方程;
(3)求三角形OAB面积的最大值。
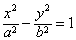 (a>b>0)和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x0,y0)引圆O的两条切线,切点分别为A,B。
(a>b>0)和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x0,y0)引圆O的两条切线,切点分别为A,B。(1)若双曲线C上存在点P,使得∠APB=90°,求双曲线离心率e的取值范围;
(2)求直线AB的方程;
(3)求三角形OAB面积的最大值。
| 解:(1)因为a>b>0, 所以 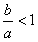 所以 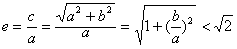 由∠APB=90°及圆的性质,可知四边形PAOB是正方形, 所以 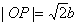 因为 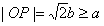 所以 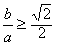 所以  故双曲线离心率e的取值范围为 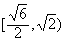 。 。(2)因为 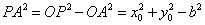 所以以点P为圆心,|PA|为半径的圆P的方程为 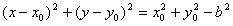 因为圆O与圆P两圆的公共弦所在的直线即为直线AB, 所以联立方程组 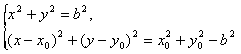 消去x2,y2,即得直线AB的方程为x0x+y0y=b2。 |
|
| (3)由(2)知,直线AB的方程为x0x+y0y=b2, 所以点O到直线AB的距离为 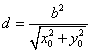 因为 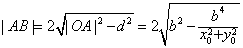  所以三角形OAB的面积 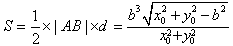 因为点P(x0,y0)在双曲线 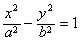 上, 上,所以 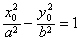 , ,即 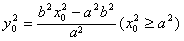 设 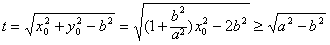 所以 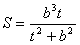 因为S' 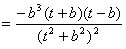 所以当0<t<b时,S'>0,当t>b时,S'<0 所以 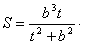 在(0,b)上单调递增,在(b,+∞)上单调递减, 当 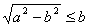 ,即 ,即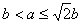 时, 时,S最大值= 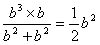 当 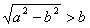 ,即 ,即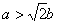 时, 时, S最大值= 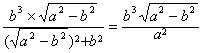 综上可知,当 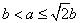 ,S最大值= ,S最大值= 当 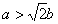 时,S最大值= 时,S最大值=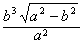 。 。 |
 |

练习册系列答案
相关题目


 (a>0,b>0)的左、右焦点分别为
(a>0,b>0)的左、右焦点分别为 、
、 ,离心率为3,直线y=2与C的两个交点间的距离为
,离心率为3,直线y=2与C的两个交点间的距离为 .
. ,证明:
,证明: 、
、 、
、 成等比数列.
成等比数列. (a>0)的一条渐近线与直线l:2x-y+1=0垂直,则实数a= .
(a>0)的一条渐近线与直线l:2x-y+1=0垂直,则实数a= .