Question

【题目】在如图所示的多面体ABCDE中，已知ABCD是边长为2的正方形，平面ABCD⊥平面ABE，∠AEB＝90°，AE＝BE.

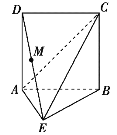
(1)若M是DE的中点，试在AC上找一点N，使得MN∥平面ABE，并给出证明；

(2)求多面体ABCDE的体积．

Answer 1

【答案】（1）见解析；（2） .

【解析】

（1）根据线面平行性质定理推得点N为AC中点，再利用线面平行判定定理给予证明，（2）先取AB的中点F，再证明EF⊥平面ABCD，最后根据锥体体积公式公式求结果.

（1）连接BD，交AC于点N，则点N即为所求，

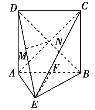
证明如下：∵ABCD是正方形，∴N是BD的中点，又M是DE的中点，∴MN∥BE，∵BE平面ABE，MN平面ABE，∴MN∥平面ABE.

(2)取AB的中点F，连接EF，∵△ABE是等腰直角三角形，且AB＝2，

∴EF⊥AB，EF＝AB＝1，∵平面ABCD⊥平面ABE，平面ABCD∩平面ABE＝AB，

EF平面ABE，∴EF⊥平面ABCD，即EF为四棱锥EABCD的高，

∴V四棱锥EABCD＝S正方形ABCD·EF＝×22×1＝.