题目内容
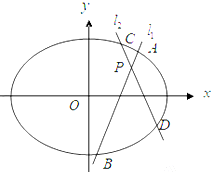 如图,已知椭圆
如图,已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
(1)求椭圆的方程;
(2)过点P(1,1)做两条倾斜角分别为a1,a2的不同的直线l1,l2,分别交椭圆与A,B,C,D,且|PA|•|PB|=|PC|•|PD|,求证:a1+a2=180°.
分析:(1)由题意得出关于参数a,b,c的方程组,解之得a,b,c的值,最后写出椭圆的方程即可;
(2)设过点P(1,1)做两条倾斜角分别为a1,a2的不同的直线l1,l2,的参数方程分别为:l1:
;l2:
.将直线l1:的参数方程代入椭圆方程结合参数t的几何意义得:|PA|•|PB|=-t1t2=-
,同理得:|PC|•|PD|=-
.最后利用|PA|•|PB|=|PC|•|PD|,即可得到a1+a2=180°.
(2)设过点P(1,1)做两条倾斜角分别为a1,a2的不同的直线l1,l2,的参数方程分别为:l1:
|
|
| 1 |
| cos 2a 1+4sin 2a 1 |
| 1 |
| cos 2a 2+4sin 2a 2 |
解答:解:(1)由题意得:
解之得:
∴椭圆的方程为:
+
=1.
(2)设过点P(1,1)做两条倾斜角分别为a1,a2的不同的直线l1,l2,的参数方程分别为:
l1:
;l2:
.
将直线l1:的参数方程代入椭圆方程得:
3(1+tcosa1)2+4(1+tsina1)2-12=0,
化简整理得:(3cos2a1+4sin2a1)t2+(6cosa1+8sina1)t-5=0,
根据参数t的几何意义得:|PA|•|PB|=-t1t2=-
,
同理得:|PC|•|PD|=-
.
由于|PA|•|PB|=|PC|•|PD|,故有:
=
,
∴cos2a1=cos2a2,sin2a1=sin2a2
∴a1+a2=180°.
|
解之得:
|
∴椭圆的方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(2)设过点P(1,1)做两条倾斜角分别为a1,a2的不同的直线l1,l2,的参数方程分别为:
l1:
|
|
将直线l1:的参数方程代入椭圆方程得:
3(1+tcosa1)2+4(1+tsina1)2-12=0,
化简整理得:(3cos2a1+4sin2a1)t2+(6cosa1+8sina1)t-5=0,
根据参数t的几何意义得:|PA|•|PB|=-t1t2=-
| 5 |
| 3cos 2a 1+4sin 2a 1 |
同理得:|PC|•|PD|=-
| 5 |
| 3cos 2a 2+4sin 2a 2 |
由于|PA|•|PB|=|PC|•|PD|,故有:
| 5 |
| 3cos 2a 1+4sin 2a 1 |
| 5 |
| 3cos 2a 2+4sin 2a 2 |
∴cos2a1=cos2a2,sin2a1=sin2a2
∴a1+a2=180°.
点评:本小题主要考查椭圆的标准方程、直线的参数方程、直线与圆锥曲线的综合问题等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.

练习册系列答案
相关题目
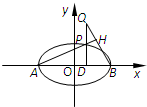 如图,已知椭圆
如图,已知椭圆 (2013•汕头一模)如图.已知椭圆
(2013•汕头一模)如图.已知椭圆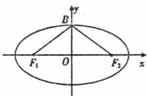 (2012•安徽模拟)如图,已知椭圆
(2012•安徽模拟)如图,已知椭圆 (2011•崇明县二模)如图,已知椭圆
(2011•崇明县二模)如图,已知椭圆 如图,已知椭圆
如图,已知椭圆