题目内容
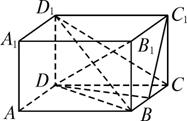
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别为CC1、AA1的中点,画出平面BED1F 与平面ABCD的交线.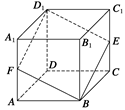

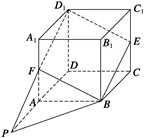
在平面AA1D1D内,延长D1F,
∵D1F与DA不平行,
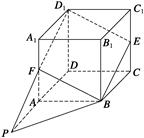
因此D1F与DA必相交于一点,设为P,
则P∈FD1,P∈DA.
又∵FD1 平面BED1F,AD
平面BED1F,AD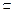 平面ABCD,
平面ABCD,
∴P∈平面BED1F,P∈平面ABCD.
又B为平面ABCD与平面BED1F的公共点,连接PB,
∴PB即为平面BED1F与平面ABCD的交线.如图所示.
∵D1F与DA不平行,

因此D1F与DA必相交于一点,设为P,
则P∈FD1,P∈DA.
又∵FD1
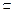 平面BED1F,AD
平面BED1F,AD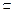 平面ABCD,
平面ABCD,∴P∈平面BED1F,P∈平面ABCD.
又B为平面ABCD与平面BED1F的公共点,连接PB,
∴PB即为平面BED1F与平面ABCD的交线.如图所示.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
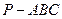 中,
中,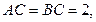 ∠
∠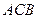 =90°,
=90°,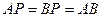 ,
,
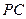 ⊥
⊥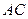 .
. (Ⅰ)求证:
(Ⅰ)求证: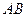 ;
; 的体积.
的体积.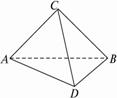
 (1)直线EF∥平面ACD;
(1)直线EF∥平面ACD; AD.
AD.
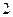 的等边△
的等边△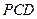 所在的平面垂直于矩形
所在的平面垂直于矩形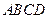 所在的平面,
所在的平面,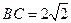 ,
,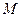 为
为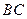 的中点.
的中点.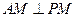 ;
;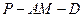 的大小.
的大小.
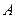 ,
,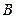 ,
,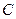 三点都是平面
三点都是平面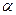 与平面
与平面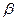 的公共点,并且
的公共点,并且