题目内容
【题目】函数![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)答案见解析;(2)![]() .
.
【解析】
(1)求出函数![]() 的定义域为
的定义域为![]() ,求得
,求得![]() ,分
,分![]() 、
、![]() 、
、![]() 三种情况讨论,分析导数的符号变化,由此可得出函数
三种情况讨论,分析导数的符号变化,由此可得出函数![]() 的单调递增区间和递减区间;
的单调递增区间和递减区间;
(2)构造函数![]() ,由题意可知
,由题意可知![]() 恒成立,对实数
恒成立,对实数![]() 分
分![]() 和
和![]() 两种情况讨论,利用导数分析函数
两种情况讨论,利用导数分析函数![]() 在区间
在区间![]() 上的单调性,验证
上的单调性,验证![]() 是否成立,由此可得出实数
是否成立,由此可得出实数![]() 的取值范围.
的取值范围.
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() .
.
(i)当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增;
上单调递增;
(ii)当![]() 时,令
时,令![]() 得
得![]() .
.
若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() .
.
①当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,
时,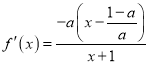 ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
综上,可得,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(2)设![]() ,
,![]() ,则
,则![]() .
.
当![]() 时,
时,![]() 单调递增,则
单调递增,则![]() .
.
所以,函数![]() 在
在![]() 上单调递增,且
上单调递增,且![]() .
.
当![]() 时,
时,![]() ,
,
于是,函数![]() 在
在![]() 上单调递增,
上单调递增,![]() 恒成立,符合题意;
恒成立,符合题意;
当![]() 时,由于
时,由于![]() ,
,![]() ,
,![]() ,
,
所以,存在![]() ,使得
,使得![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
故![]() ,不符合题意,
,不符合题意,
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.

【题目】2019年1月1日,我国开始施行《个人所得税专项附加扣除操作办法》,附加扣除的专项包括子女教育、继续教育、大病医疗、住房货款利息、住房租金、赡养老人.某单位有老年员工140人,中年员工180人,青年员工80人,现采用分层抽样的方法,从该单位员工中抽取20人,调查享受个人所得税专项附加扣除的情况,并按照员工类别进行各专项人数汇总,数据统计如下:
员工\人数\专项 | 子女教育 | 继续教育 | 大病医疗 | 住房贷款利息 | 住房租金 | 赡养老人 |
老员工 | 4 | 0 | 2 | 2 | 0 | 3 |
中年员工 | 8 | 2 | 1 | 5 | 1 | 8 |
青年员工 | 1 | 2 | 0 | 1 | 2 | 1 |
(Ⅰ)在抽取的20人中,老年员工、中年员工、青年员工各有多少人;
(Ⅱ)从上表享受住房货款利息专项扣除的员工中随机选取2人,求选取2人都是中年员工的概率.
【题目】已知椭圆![]() 的焦点在
的焦点在![]() 轴上,中心在坐标原点,抛物线
轴上,中心在坐标原点,抛物线![]() 的焦点在
的焦点在![]() 轴上,顶点在坐标原点,在
轴上,顶点在坐标原点,在![]() 、
、![]() 上各取两个点,将其坐标记录于表格中:
上各取两个点,将其坐标记录于表格中:
|
|
|
|
|
|
|
|
|
|
(1)求![]() 、
、![]() 的标准方程;
的标准方程;
(2)已知定点![]() ,
,![]() 为抛物线
为抛物线![]() 上的一动点,过点
上的一动点,过点![]() 作抛物线
作抛物线![]() 的切线交椭圆
的切线交椭圆![]() 于
于![]() 、
、![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.