题目内容
如图,在三棱锥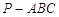 中,
中,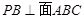 ,
,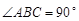 ,
,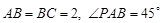 ,点
,点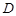 、
、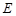 、
、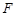 分别为
分别为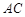 、
、 、
、 的中点.
的中点.
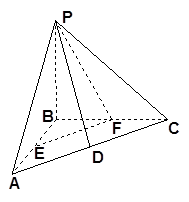
(1)求直线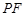 与平面
与平面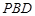 所成角的正弦值;
所成角的正弦值;
(2)求二面角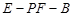 的大小.
的大小.
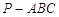 中,
中,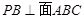 ,
,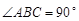 ,
,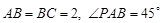 ,点
,点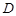 、
、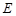 、
、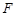 分别为
分别为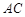 、
、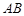 、
、 的中点.
的中点.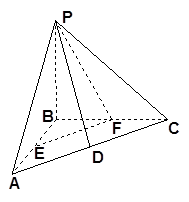
(1)求直线
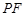 与平面
与平面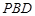 所成角的正弦值;
所成角的正弦值;(2)求二面角
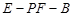 的大小.
的大小.(1)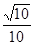 (2)二面角
(2)二面角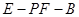 的正切值为
的正切值为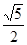
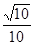 (2)二面角
(2)二面角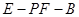 的正切值为
的正切值为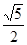
试题分析:解:(法一)(1)连接
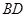 ,与
,与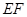 的交点为
的交点为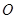 ,在
,在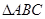 中,
中, 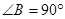 .
.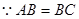 ,点
,点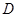 为
为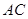 的中点,
的中点,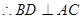 .又
.又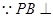 面
面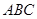 ,则
,则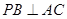 .
.则
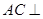 面
面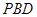 ,而
,而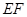 ∥
∥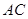 ,则
,则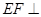 面
面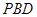 ,
,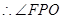 为直线
为直线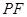 与平面
与平面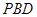 所成的角,
所成的角, 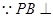 面
面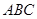 ,
,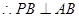 ,
,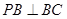 .
.又
 ,
,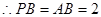 .
.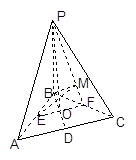
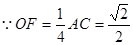 ,
,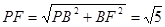 ,
,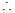 在
在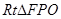 中,
中,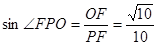 ,
, 直线与平面所成角的正弦值为
直线与平面所成角的正弦值为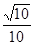 6分
6分(2)过点
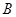 作
作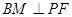 于点
于点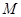 ,连接
,连接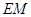 ,
,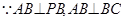 ,
,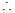
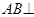 平面
平面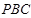 ,即
,即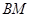 为
为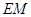 在平面
在平面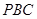 内的射影,
内的射影,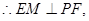
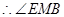 为二面角
为二面角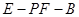 的平面角.
的平面角.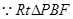 中,
中,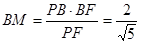 ,
,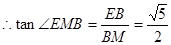 ,
,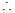 二面角
二面角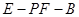 的正切值为
的正切值为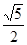 . 12分
. 12分(法二)建立间直角坐标系如图,则
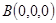 ,
,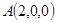 ,
,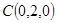 ,
,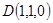 ,
,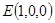
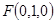 ,
,

(1)由已知可得,
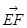 =
=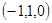 为平面
为平面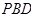 的法向量
的法向量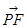 =
=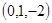 ,
,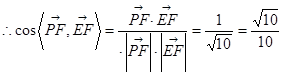 .
.直线
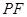 与面
与面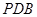 所成角的正弦值为
所成角的正弦值为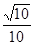 . 6分
. 6分(2)设平面
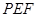 的法向量为
的法向量为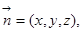 ,
, ,
,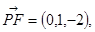
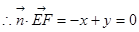 ,
,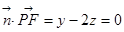 ,令
,令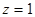 ,
,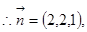
由已知可得,向量
 为平面
为平面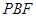 的一个法向量,
的一个法向量, 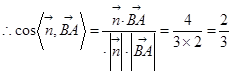
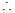 二面角
二面角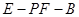 为
为 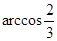 . 12分
. 12分点评:解决的关键是熟练的根据判定定理和性质定理来得到角,结合三角形求解,或者利用向量法来求解,属于中档题。

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 中,四边形
中,四边形 是正方形,
是正方形, 平面
平面 ∥
∥

 与
与 所成角的余弦值;
所成角的余弦值; 平面
平面 ;
; 的正切值。
的正切值。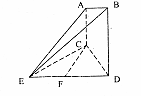
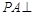 平面ABCD,
平面ABCD,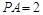 ,E是PC上的一点.
,E是PC上的一点.
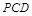 ;
;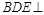 平面
平面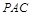 ;
;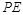 为多长时,
为多长时,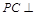 平面
平面 ?
?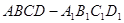 中,面
中,面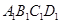 中心为
中心为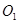 .
.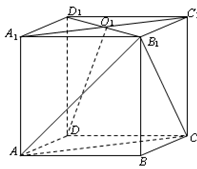
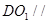 面
面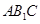 ;
;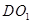 与
与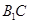 所成角.
所成角.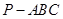 中,
中,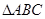 是底面,
是底面,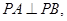
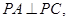
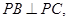 且这四个顶点都在半径为2的球面上,
且这四个顶点都在半径为2的球面上,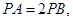 则这个三棱锥的三个侧棱长的和的最大值为( )
则这个三棱锥的三个侧棱长的和的最大值为( )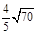
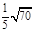
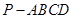 中,
中,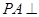 平面
平面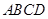 ,四边形
,四边形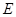 ,
,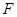 分别是
分别是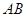 ,
,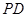 的中点.若
的中点.若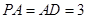 ,
,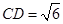 。
。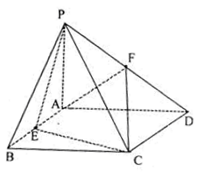
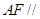 平面
平面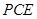 ;
;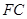 平面
平面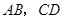 的长度分别等于
的长度分别等于 分别为
分别为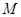 ;②弦
;②弦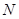 ;
;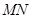 的最大值为5; ④
的最大值为5; ④