题目内容
在平面直角坐标系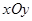 中,已知椭圆
中,已知椭圆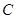 的中心在原点
的中心在原点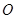 ,焦点在
,焦点在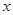 轴上,短轴长为
轴上,短轴长为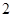 ,离心率为
,离心率为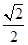 .
.
(I)求椭圆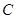 的方程;
的方程;
(II)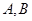 为椭圆
为椭圆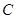 上满足
上满足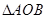 的面积为
的面积为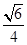 的任意两点,
的任意两点,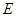 为线段
为线段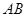 的中点,射线
的中点,射线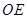 交椭圆
交椭圆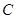 与点
与点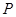 ,设
,设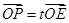 ,求实数
,求实数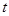 的值.
的值.
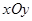 中,已知椭圆
中,已知椭圆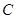 的中心在原点
的中心在原点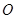 ,焦点在
,焦点在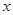 轴上,短轴长为
轴上,短轴长为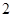 ,离心率为
,离心率为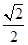 .
.(I)求椭圆
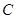 的方程;
的方程;(II)
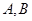 为椭圆
为椭圆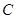 上满足
上满足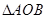 的面积为
的面积为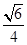 的任意两点,
的任意两点,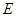 为线段
为线段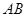 的中点,射线
的中点,射线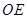 交椭圆
交椭圆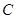 与点
与点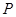 ,设
,设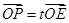 ,求实数
,求实数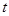 的值.
的值.(I) 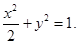 (Ⅱ)
(Ⅱ) 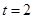 或
或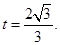
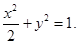 (Ⅱ)
(Ⅱ) 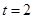 或
或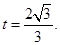
(I)设椭圆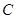 的方程为
的方程为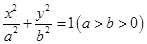 ,
,
由题意知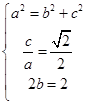 ,解得
,解得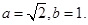
因此椭圆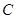 的方程为
的方程为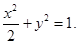
(II)(1)当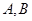 两点关于
两点关于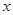 轴对称时,
轴对称时,
设直线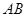 的方程为
的方程为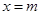 ,由题意知
,由题意知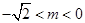 或
或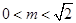 ,
,
将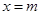 代入椭圆方程
代入椭圆方程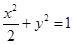 得
得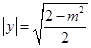 .
.
所以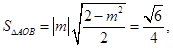
解得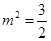 或
或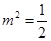 .
.
又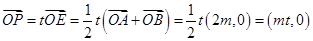 ,
,
因为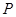 为椭圆
为椭圆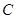 上一点,所以
上一点,所以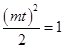 ,
,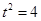 或
或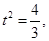
又因为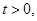 所以
所以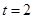 或
或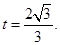
(2)当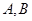 两点关于
两点关于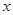 轴不对称时,
轴不对称时,
设直线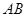 的方程为
的方程为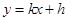 ,将其代入椭圆方程
,将其代入椭圆方程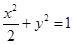 得
得
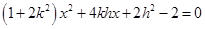 .
.
设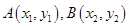 ,由判别式
,由判别式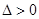 可得
可得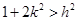 ,
,
此时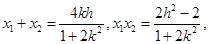
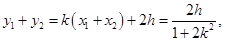
所以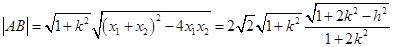 ,
,
因为点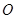 到直线
到直线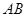 的距离为
的距离为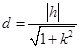 ,
,
所以
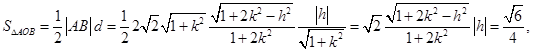
令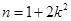 ,则
,则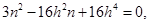
解得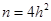 或
或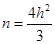 ,即
,即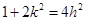 或
或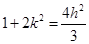 .
.
又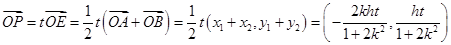 ,
,
因为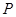 为椭圆
为椭圆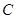 上一点,所以
上一点,所以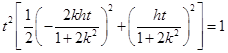 ,
,
即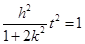 ,所以
,所以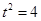 或
或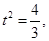
又因为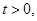 所以
所以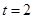 或
或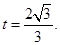
经检验,适合题意.
综上可知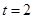 或
或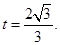
【考点定位】本题基于椭圆问题综合考查椭圆的方程、直线和椭圆的位置关系、平面向量的坐标运算等知识,考查方程思想、分类讨论思想、推理论证能力和运算求解能力.第一问通过椭圆的性质确定其方程,第二问根据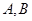 两点关于
两点关于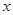 轴的对称关系进行分类讨论,分别设出直线
轴的对称关系进行分类讨论,分别设出直线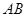 的方程,通过联立、判断
的方程,通过联立、判断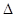 、消元等一系列运算“动作”达成目标.本题极易简单考虑设直线
、消元等一系列运算“动作”达成目标.本题极易简单考虑设直线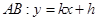 的形式而忽略斜率不存在的情况造成漏解.在联立方程得到
的形式而忽略斜率不存在的情况造成漏解.在联立方程得到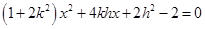 后,后续运算会多次出现
后,后续运算会多次出现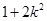 这一式子,换元简化运算不失为一种好方法,令
这一式子,换元简化运算不失为一种好方法,令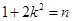 ,搭建了
,搭建了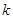 与
与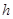 的桥梁,使坐标的代入运算更为顺畅,使“化繁为简”这一常用原则得以完美呈现.
的桥梁,使坐标的代入运算更为顺畅,使“化繁为简”这一常用原则得以完美呈现.
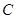 的方程为
的方程为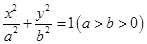 ,
,由题意知
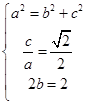 ,解得
,解得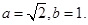
因此椭圆
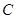 的方程为
的方程为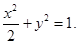
(II)(1)当
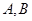 两点关于
两点关于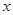 轴对称时,
轴对称时,设直线
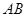 的方程为
的方程为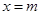 ,由题意知
,由题意知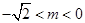 或
或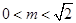 ,
,将
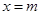 代入椭圆方程
代入椭圆方程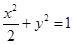 得
得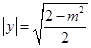 .
.所以
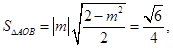
解得
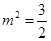 或
或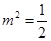 .
.又
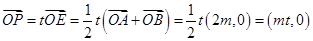 ,
,因为
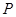 为椭圆
为椭圆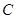 上一点,所以
上一点,所以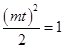 ,
,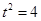 或
或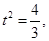
又因为
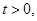 所以
所以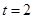 或
或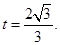
(2)当
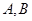 两点关于
两点关于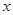 轴不对称时,
轴不对称时,设直线
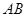 的方程为
的方程为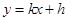 ,将其代入椭圆方程
,将其代入椭圆方程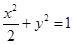 得
得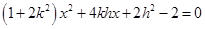 .
.设
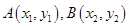 ,由判别式
,由判别式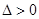 可得
可得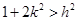 ,
,此时
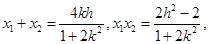
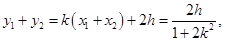
所以
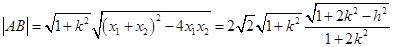 ,
,因为点
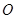 到直线
到直线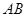 的距离为
的距离为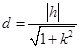 ,
,所以
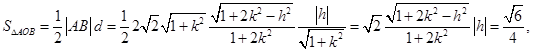
令
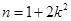 ,则
,则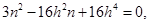
解得
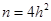 或
或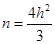 ,即
,即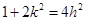 或
或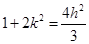 .
.又
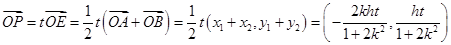 ,
,因为
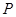 为椭圆
为椭圆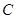 上一点,所以
上一点,所以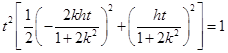 ,
,即
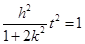 ,所以
,所以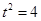 或
或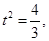
又因为
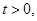 所以
所以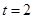 或
或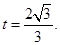
经检验,适合题意.
综上可知
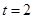 或
或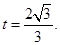
【考点定位】本题基于椭圆问题综合考查椭圆的方程、直线和椭圆的位置关系、平面向量的坐标运算等知识,考查方程思想、分类讨论思想、推理论证能力和运算求解能力.第一问通过椭圆的性质确定其方程,第二问根据
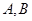 两点关于
两点关于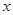 轴的对称关系进行分类讨论,分别设出直线
轴的对称关系进行分类讨论,分别设出直线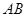 的方程,通过联立、判断
的方程,通过联立、判断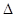 、消元等一系列运算“动作”达成目标.本题极易简单考虑设直线
、消元等一系列运算“动作”达成目标.本题极易简单考虑设直线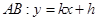 的形式而忽略斜率不存在的情况造成漏解.在联立方程得到
的形式而忽略斜率不存在的情况造成漏解.在联立方程得到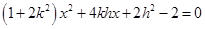 后,后续运算会多次出现
后,后续运算会多次出现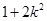 这一式子,换元简化运算不失为一种好方法,令
这一式子,换元简化运算不失为一种好方法,令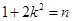 ,搭建了
,搭建了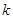 与
与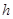 的桥梁,使坐标的代入运算更为顺畅,使“化繁为简”这一常用原则得以完美呈现.
的桥梁,使坐标的代入运算更为顺畅,使“化繁为简”这一常用原则得以完美呈现.
练习册系列答案
相关题目
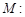
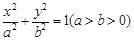 的四个顶点恰好是一边长为2,一内角为
的四个顶点恰好是一边长为2,一内角为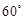 的菱形的四个顶点.
的菱形的四个顶点. 的方程;
的方程;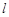 与椭圆
与椭圆 ,
,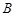 两点,且线段
两点,且线段 的垂直平分线经过点
的垂直平分线经过点 ,求
,求 (
( 为原点)面积的最大值.
为原点)面积的最大值.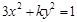 的一个焦点坐标为
的一个焦点坐标为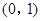 ,则其离心率等于 ( )
,则其离心率等于 ( )
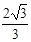

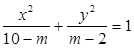 的长轴在
的长轴在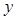 轴上,且焦距为4,则
轴上,且焦距为4,则 等于( )
等于( )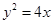 的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于x轴,垂足为T,与抛物线交于不同的两点P、Q且
的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于x轴,垂足为T,与抛物线交于不同的两点P、Q且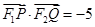 .
.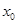 ;
;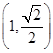 .
.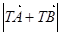 的取值范围.
的取值范围.  中,若
中,若
 右顶点,则常数
右顶点,则常数 .
.
 ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线 的焦点重合, 则此椭圆方程为
的焦点重合, 则此椭圆方程为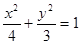



 的离心率为
的离心率为 ,且过点(
,且过点( ),
), 与椭圆交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:△OPQ面积的最大值及此时直线的方程.
与椭圆交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:△OPQ面积的最大值及此时直线的方程.