题目内容
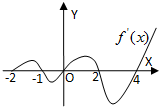
已知函数f（x）的定义域为[-2，+∞），部分对应值如下表，函数y=f′（x）的大致图象如下图所示，则函数y=f（x）在区间[-2，4]上的零点个数为（ ）
| x | -2 | 0 | 4 |
| f（x） | 0 | -1 | 0 |
| A．2 | B．3 | C．4 | D．5 |
由函数y=f′（x）的大致图象、导数的符号可得，
x=-1是函数f（x）的极大值点，
x=0是函数f（x）的极小值点，
x=2是函数f（x）的极大值点，
x=4是函数f（x）的极小值点．
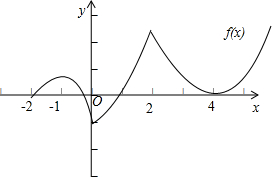
再根据导函数的图象和原函数的关系以及题中所给的表格可得原函数的大致图象如图：
结合原函数f（x）的图象可得函数y=f（x）在区间[-2，4]上的零点个数为4，
故选 C．
x=-1是函数f（x）的极大值点，
x=0是函数f（x）的极小值点，
x=2是函数f（x）的极大值点，
x=4是函数f（x）的极小值点．
再根据导函数的图象和原函数的关系以及题中所给的表格可得原函数的大致图象如图：
结合原函数f（x）的图象可得函数y=f（x）在区间[-2，4]上的零点个数为4，
故选 C．
练习册系列答案
阅读快车系列答案
相关题目
，其中x是校服的月产量，问：（1）将利润表示为关于月产量x的函数
．（2）当月产量为何值时，工厂所获利润最大?最大利润为多少元?（总收益=总成本+利润）
（
）的两个根都大于1的充要条件 .