题目内容
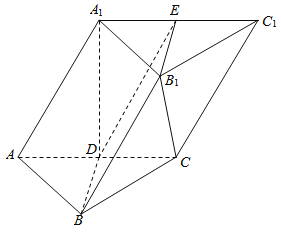
【题目】将边长为2的正![]() 沿着高
沿着高![]() 折起,使
折起,使![]() ,若折起后
,若折起后![]() 四点都在球
四点都在球![]() 的表面上,则球
的表面上,则球![]() 的表面积为( )
的表面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
通过底面三角形BCD求出底面圆的半径DM,判断球心到底面圆的距离OM,求出球O的半径,即可求解球O的表面积.
△BCD中,BD=1,CD=1,∠BDC=120°,
底面三角形的底面外接圆圆心为M,半径为:r,由余弦定理得到BC=![]() ,再由正弦定理得到
,再由正弦定理得到![]()
见图示:
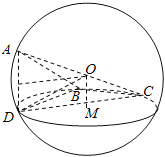
AD是球的弦,DA=![]() ,将底面的圆心M平行于AD竖直向上提起,提起到AD的高度的一半,即为球心的位置O,∴OM=
,将底面的圆心M平行于AD竖直向上提起,提起到AD的高度的一半,即为球心的位置O,∴OM=![]() ,在直角三角形OMD中,应用勾股定理得到OD,OD即为球的半径.∴球的半径OD=
,在直角三角形OMD中,应用勾股定理得到OD,OD即为球的半径.∴球的半径OD=![]() .
.
该球的表面积为:4π×OD2=7π;
故选:B.

练习册系列答案
相关题目